在庫最適化モジュール optinv と安全在庫配置システム MESSA
Streamlitで作成した簡易システムの紹介ビデオ
安全在庫配置システム: MESSA (MEta Safety Stock Allocation system)
はじめに
需要の不確実性に対処するための在庫が安全在庫である. 1拠点の安全在庫は古典であり,簡単な「公式」もしくはシミュレーションによって最適化できる. ここでは,サプライ・チェイン全体を考えて,各在庫地点の安全在庫を決定するための方策のパラメータの最適化を考える.
多くの研究者の長年の努力にも関わらず,多拠点での一般ネットワーク型の在庫最適化モデルはいまだ未解決の部分も多い. ここでは,適切に付加した仮定の下で,幾つかの最適化モデルを構築する.
基礎理論
サービスレベルと安全在庫係数
ここでは,小売店に顧客がやってくることによって需要が発生する場合を考える. 顧客は,毎日小売店にやってきて商品を購入するが,その量は気分によって変わるものとする. 一般には,商品が品切れしてしまうことは避けなければならない. 商品を余分に在庫しておく費用が,品切れしてしまう費用より小さい場合には, 商品を余分に在庫して気まぐれな顧客のために準備しておくことが常套手段である. このように,需要の不確実性に対処するためにもつ在庫を安全在庫(safety inventory, safety stock)とよぶ.
いま,簡単のため,毎日の需要量は,定常な分布にしたがっているものとする. ここで「定常」とは,日によって需要の分布が変化しないことを指す. 分布によっては,負の需要量になる可能性があるが,その場合には需要量を \(0\) と定義する. たとえば, 需要が正規分布と仮定した場合には,負の部分を除いた正規分布(切断正規分布)を指すものとする.
Excelインターフェイス
在庫最適化用のExcelテンプレートを生成する関数 make_excel_messa
返値:
- wb: 在庫最適化用のExcel Workbook
make_excel_messa
make_excel_messa ()
make_excel_messa関数の使用例
wb = make_excel_messa()
wb.save("messa-templete.xlsx")Excel Workbookからデータフレームを生成する関数 prepare_df_for_messa
引数: - wb: Excel Workbook
返値:
- stsge_df : 点の情報を保管したデータフレーム
- bom_df : 枝の情報を保管したデータフレーム
prepare_df_for_messa
prepare_df_for_messa (wb)
Excel Workbookから最適化用のデータを準備する関数 prepare_opt_for_messa
引数: - wb: Excel Workbook
返値: - G: 閉路を含まない有向グラフ - ProcTime: 処理時間(NumPyの配列);以下の配列はグラフGの点を列挙したときの順序(グラフに点を追加した順序)の順に保管してあるものとする. - LTUB: 保証リード時間上限(NumPyの配列) - z: 安全在庫係数 - mu: 需要の平均(NumPyの配列) - sigma: 需要の標準偏差(NumPyの配列) - h: 在庫費用(NumPyの配列)
prepare_opt_for_messa
prepare_opt_for_messa (wb)
prepare_opt_for_messaの使用例
# wb = load_workbook("messa-ex2.xlsx")
# G, ProcTime, LTUB, z, mu, sigma, h = prepare_opt_for_messa(wb)
#best_cost, best_sol, best_NRT, best_MaxLI, best_MinLT = tabu_search_for_SSA(G, ProcTime, LTUB, z, mu, sigma, h, max_iter = 10, TLLB =1, TLUB =3, seed = 1)安全在庫配置の最適化し,Excelシートを生成する関数 messa_for_excel
引数: - wb: Excel Workbook - best_NRT: 最良解における正味補充時間(在庫日数) - best_MaxLI: 最良解における最大補充リード時間 - best_MinLT: 最良解における最小保証リード時間
返値: - wb: Excel Workbook
messa_for_excel
messa_for_excel (wb, best_NRT, best_MaxLI, best_MinLT)
messa_for_excel関数の使用例
# wb = load_workbook("messa-ex1.xlsx")
# G, ProcTime, LTUB, z, mu, sigma, h = prepare_opt_for_messa(wb)
# best_cost, best_sol, best_NRT, best_MaxLI, best_MinLT = tabu_search_for_SSA(G, ProcTime, LTUB, z, mu, sigma, h, max_iter = 10, TLLB =1, TLUB =3, seed = 1)
# wb = messa_for_excel(wb, best_NRT, best_MaxLI, best_MinLT )
# wb.save("messa-ex1-result.xlsx")# n_samples =100
# n_periods =100
# for i in range(n):
# if best_NRT[i]>=1:
# s, S = approximate_ss(mu[i], sigma[i], best_NRT[i]-1, b[i], h[i], fc[i])
# print(s,S)
# cost, I = simulate_inventory(n_samples =n_samples, n_periods =n_periods, mu=mu[i], sigma=sigma[i], LT=int(best_NRT[i]), Q=None, R=s, b=b[i], h=h[i], fc=fc[i], S=S)# print(cost)Pyvizの図を生成する関数 generate_pyvis_for_messa
引数:
- wb: Excel Workbook
- G: 閉路を含まない有向グラフ
- best_cost:最良値
- best_sol: 最良解(在庫を保持するなら1、否なら0の配列)
- best_MaxLI: 最良解における最大補充リード時間
- best_MinLT: 最良解における最小保証リード時間
- notebook: Jupyter用の図を生成するとき True (既定値 True)
返値:
- net: pyvisの図オブジェクト
generate_pyvis_for_messa
generate_pyvis_for_messa (wb, G, best_sol=None, best_MaxLI=None, best_MinLT=None, notebook=True)
generate_pyvis_for_messa関数の使用例
#net = generate_pyvis_for_messa(wb, G, best_sol, best_MaxLI, best_MinLT)
#net.show("example.html")需要予測と合わせた動的在庫最適化
発注固定費用を考えない場合
#hide
需要予測 \(\hat{y}_t\) と需要量 \(y_t\) の差(誤差)を \(e_t\) とし, 定常性を仮定する. この分布を,平均 \(0\),標準偏差 \(\sigma\) の正規分布とすると,基在庫レベル \(S = z \sigma \sqrt{NRT}\) が定まる. ただし \(z\) は安全在庫係数である.
ここで \(NRT\) は正味補充時間であり,補充リード時間 \(RLT\) から保証リード時間 \(GLT\) を減じたものと定義される.
安全在庫のための発注量 \(Q_t\) と予測に基づく動的な需要のための発注量を分けて考える.
安全在庫のための在庫方策は,予測誤差 \(e_t\) を需要とした基在庫方策になる.
- \(IP_t\): 期首在庫ポジション; 期末在庫ポジション(常に \(S\))から需要量 \(e_t\) を減じた値
\[ IP_t = S -e_t \]
- \(Q_t\): 安全在庫分の発注量; \(S-IP_t\) と設定する. 負の値もとる.
\[ Q_t = S-IP_t = S -(S-e_t) = e_t \]
つまり,誤差の分だけ発注すれば良い.
- \(O_t\): 動的な需要を考慮した発注量; リード時間後の需要の予測値 \(\hat{d}_{t+RLT-GLT}\) 分だけ発注するものとする. 負の場合も考えられるが,その場合には \(0\) とし, 次の期の発注量から減じる.
\[ O_t = [ \hat{d}_{t+RLT-GLT} + Q_t ]^+ \]
\(\hat{d}_{t+RLT-GLT} + Q_t <0\) のとき: \[ e_{t+1} := e_{t+1} + \hat{d}_{t+RLT-GLT} + Q_t \]
在庫のフローは以下の式で得られる.
\[ I_{t-1} + O_{t-RLT} - d_{t-GLT} = I_t \]
初期在庫量は, 過去の発注量がすべて \(0\) と仮定したとき, 安全在庫量 \(S\) に\(\sum_{t=-GLT}^{RLT} \hat{d}_{t}\) を加えたものとする.
\[ I_0 = \sum_{t=-GLT}^{RLT} \hat{d}_{t} + S \]
発注固定費用を考慮した場合
#hide
発注費用を考慮した場合では,動的な需要に対して動的ロットサイズ決定問題を解いて,発注量を決める.
サイクル時間 \(CT\) は,需要を定常と仮定したときの発注間隔であり,経済発注量の公式で簡単に求めることができる. 安全在庫分は,サイクル時間 \(CT\) と正味補充時間 \(NRT\) の大きい方を \(L\) としたとき,安全在庫係数 \(z\) と検証期間における予測誤差の標準偏差 \(\sigma\) を用いて,以下のように決める.
\[ z \sigma \sqrt{T} \]
\(O_t\): 動的な需要を考慮した発注量; まず,需要の予測値 \(\hat{d}\) に対して動的ロットサイズ決定問題を解くことによって求める. それを正味補充時間 \(NRT\) 分だけ前にずらすことによって \(O_t\) を決める.
\(O'_t\): 誤差補正した発注量; 需要予測 \(\hat{y}_t\) と需要量 \(y_t\) の差(誤差)を \(e_t\) を保存し,その累積値 \(E_t\) を計算する. 動的発注量 \(O_t\) が正なら, \([O_t+E_{t-1}]^+\) を \(O'_t\) とし, 累積量を \(0\) に戻す. ただし,誤差補正発注量が負になる場合には,その分だけ累積誤差に加えておく.
式で表すと以下のようになる.
\[ O'_t = \left\{ \begin{array}{ll} [O_t+E_t]^+ & O_t > 0 \\ 0 & O_t = 0 \end{array} \right. \]
\[ E_t = \left\{ \begin{array}{ll} e_t & O_t > 0, O_t+E_{t-1} \geq 0 \\ O_t+E_{t-1}+e_t & O_t > 0, O_t+E_{t-1} < 0 \\ E_{t-1} + e_t & O_t = 0 \end{array} \right. \]
在庫量は,補充リード時間を \(RLT\),保証リード時間を \(GLT\) としたとき, 以下の式で得られる.
\[ I_{t-1} + O'_{t-RLT} - d_{t-GLT} = I_t \]
Wagner-Whitin法による動的ロットサイズ決定問題の求解関数 ww
動的ロットサイズ決定モデルの最適化(モデルについては動的ロットサイズ決定モデルlotsize参照)
需要予測に基づく不確実性を考慮した在庫最適化(forecast)で利用
引数: - demand: 多期間需要を表すリスト - fc: 固定費用(定数かリスト); 関数内で需要と同じ長さのNumPy配列に変換される. - vc: 変動費用(定数かリスト); 関数内で需要と同じ長さのNumPy配列に変換される. - h: 在庫費用(定数かリスト); 関数内で需要と同じ長さのNumPy配列に変換される.
返値: - cost: 最適値 - order: 各期の発注量を入れたリスト
ww
ww (demand, fc=100.0, vc=0.0, h=5.0)
ww関数の使用例
fixed= 3
variable= [1,1,3,3,3]
h = 1.
demand=[5,7,3,6,4]
ww(demand, fc =fixed, vc=variable, h=h)(57.0, array([ 5., 16., 0., 0., 4.]))分布に最もよく適合した連続確率分布を求める関数 best_distribution
定常分布をもつ需要データに最もよく合う連続確率分布を求める.
引数: - data: データの配列
返値:
- fig: データの度数分布表(ヒストグラム)と最良誤差分布の密度関数の図(適合する分布がない場合には,度数分布表のみ)
- frozon_dist: 最良誤差分布(パラメータ固定)
- best_fit_name: 最良誤差分布の名前
- best_fit_params: 最良誤差のパラメータ
best_distribution
best_distribution (data)
best_distribution関数の適用例
# data = np.random.normal(100,10,1000)
# fig, best_dist, best_fit_name, best_fit_params = best_distribution(data)
# plotly.offline.plot(fig);
# print(best_fit_name, best_fit_params)powerlognorm (11.799333308942117, 0.20671017783771561, 16.468598592930654, 116.65707079233306)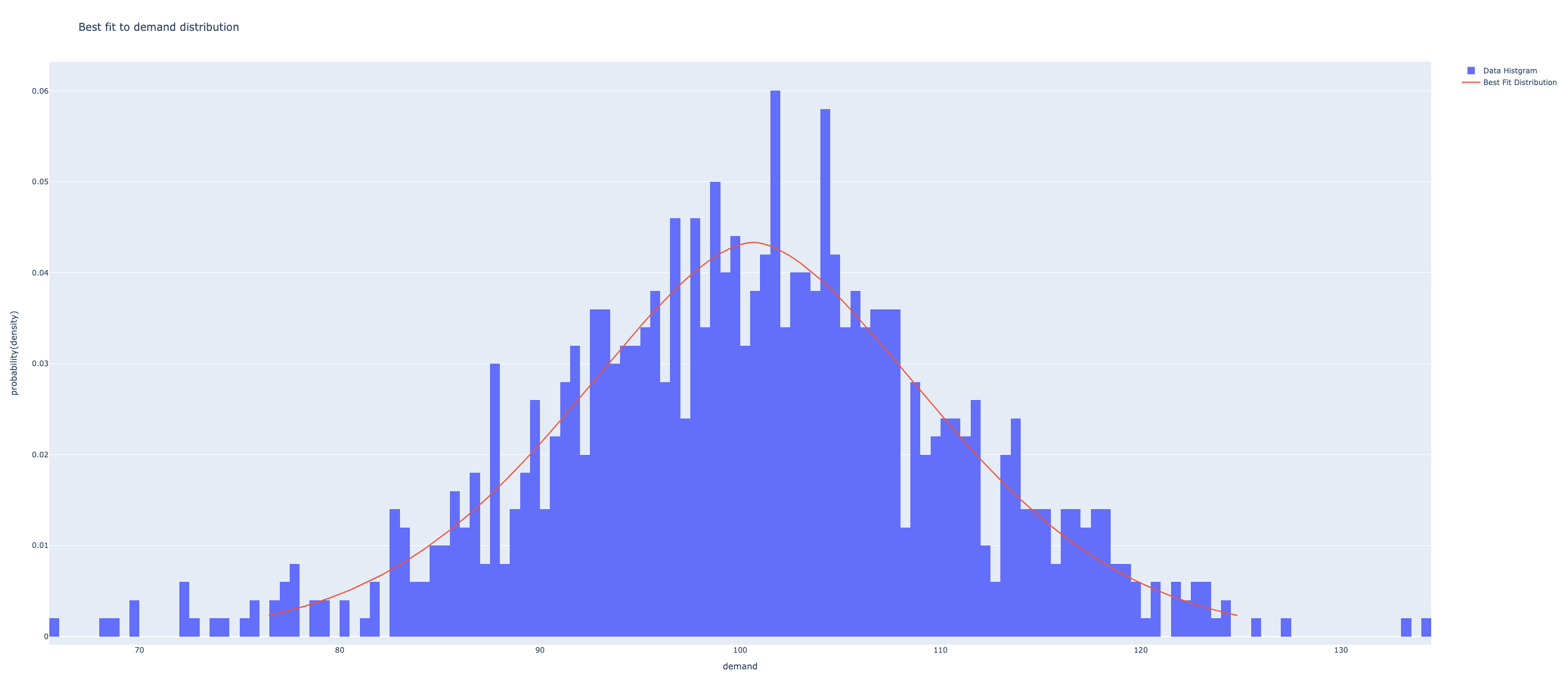
分布に適合した表形式の確率分布を求める関数 best_histogram
定常分布をもつ需要データから表形式(度数分布)による確率分布を求める. データ数が少ない(50未満)の場合には,平均値を合わせるため左に0.5だけ\(x\)軸の区分をシフトさせる.
引数: - data: データの配列 - nbins: ビン数(既定値は50とデータ数の小さい方)
返値:
- fig: データの度数分布表(ヒストグラム)と分布の密度関数の図
- hist_dist: 度数分布(パラメータ固定)
best_histogram
best_histogram (data, nbins=50)
best_histogram関数の適用例
data = np.random.normal(100,10,1000)
fig, hist_dist = best_histogram(data, nbins = 20)
plotly.offline.plot(fig);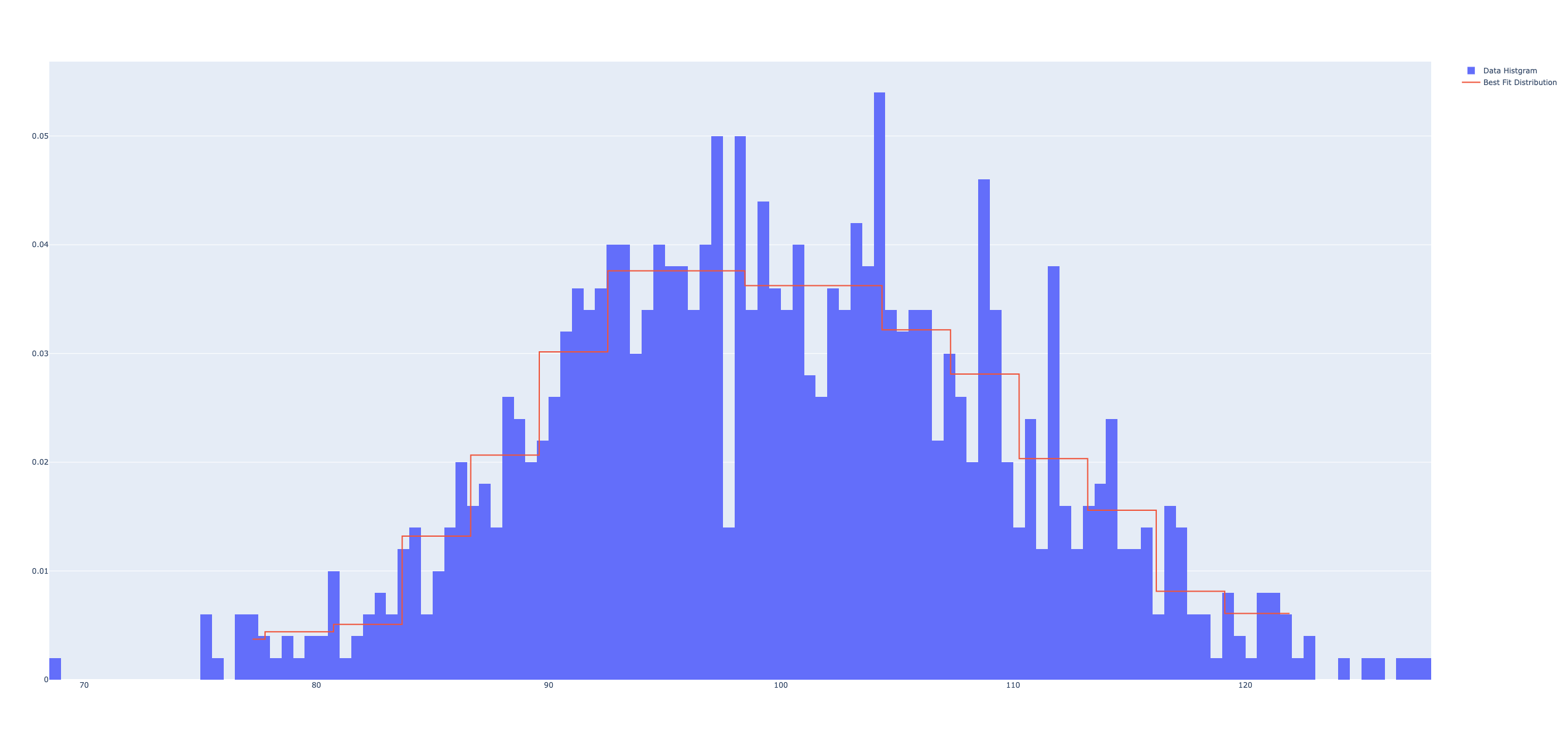
得られた分布に基いてランダムな需要を発生させる.
#best_dist.mean(),hist_dist.mean()(100.48413228614606, 100.20054738268533)得られた分布に対して,在庫管理に必要な統計量を計算する.
# print( best_dist.ppf(0.9), hist_dist.ppf(0.9) ) #90%品切れしないための在庫量
# print( best_dist.sf(200), hist_dist.sf(200) ) #在庫が200のときの品切れ率112.80769882762985 112.77535790405301
0.0 0.0需要分布に対して最適な適合をもつ分布を返す関数 fit_demand
引数: - demand_df: 需要データフレーム - cust_selected: 需要の分布を求めたい顧客名のリスト - prod_selected: 需要の分布を求めたい製品名のリスト - agg_period: 集約を行う期。例えば1週間を1期とするなら”1w”とする。既定値は1日(“1d”) - nbins: ヒストグラムのビン数(既定値は50) - L: リード時間(在庫管理で用いる.L日前からL-1前の需要の合計の分布をとる.)
返値: - dic: 顧客名と製品名のタプルをキーとし,分布の情報を値とした辞書; 分布の情報は以下のタプル
- fig: 誤差が最小の分布の密度関数と度数分布表の図
- fig2: 近似的な表形式の確率関数と度数分布表の図
- best_dist: 誤差最小の分布の密度関数
- hist_dist: 度風分布表のデータから構成された確率関数
- best_fit_name: 誤差最小の分布名
- best_fit_params: 誤差を最小にする分布のパラメータ
fit_demand
fit_demand (demand_df, cust_selected, prod_selected, agg_period='1d', nbins=50, L=1)
需要分布の推定(顧客と製品に対して):リード時間Lを入力とし,その間の需要の分布を計算する必要がある!
fit_demand関数の適用例
# demand_df = pd.read_csv(folder+"demand.csv")
# #demand_df = pd.read_csv(folder+"demand_all.csv")
# cust_selected = [ demand_df["cust"].iloc[11]]
# prod_selected = [ demand_df["prod"].iloc[1] ]
# #cust_selected = ["前橋市"]
# #prod_selected = ["F"]
# #print(cust_selected, prod_selected)
# dic = fit_demand(demand_df, cust_selected, prod_selected, agg_period ="1d", nbins=50, L=3)# if dic[ cust_selected[0], prod_selected[0] ] is not None:
# fig, fig2, best_dist, hist_dist, best_fit_name, best_fit_params = dic[ cust_selected[0], prod_selected[0] ]
# print(best_fit_name, best_fit_params)
# plotly.offline.plot(fig);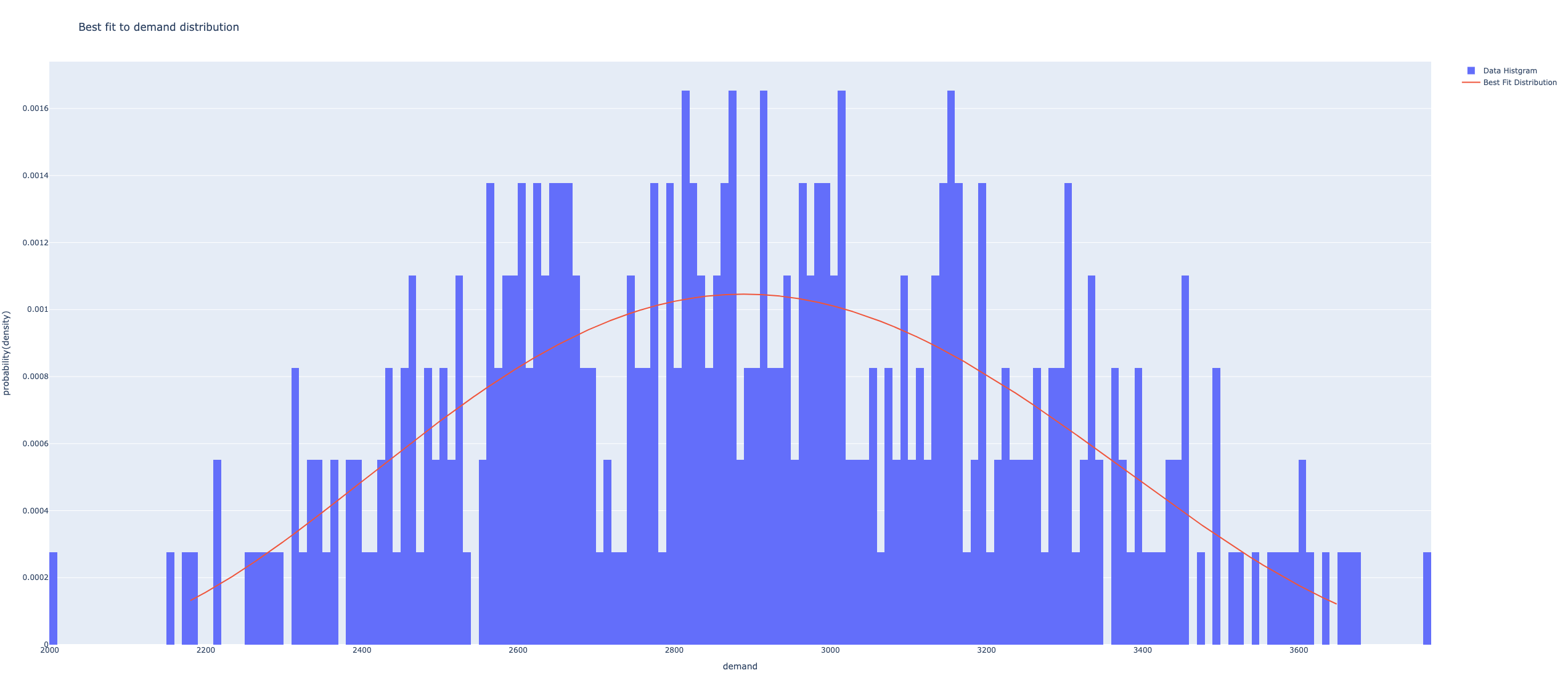
経済発注量モデル
EOQ公式(economic ordering quantity formula)
- 需要量は1日あたり \(d\) 単位である.
- 発注の際には,発注量によらない固定的な費用(これを発注費用とよぶ) \(K\) 円が課せられる.
- 在庫保管費用は保管されている在庫量に比例してかかり, 品目 \(1\) 個あたりの保管費用は \(1\)日で \(h\) 円とする.
最適発注量: \[ Q^* = \sqrt{ \frac{2Kd}{h} } \]
最適値: \[ \sqrt{ 2 K h d} \]
バックオーダーを考慮
- 品切れ費用はバックオーダーの量に比例してかかり, 品目 \(1\) 個あたりの品切れ費用は \(1\) 日あたり \(b\) 円とする.
臨界率(critical ratio): \[ \omega = \frac{b}{b+h} \]
最適値: \[ \sqrt{ 2 K h d \omega} \]
最適発注量: \[ Q^* =\sqrt{ \frac{2Kd}{h \omega} } \]
数量割引の考慮
増分割引(incremental discount): ある一定数量を超えると, 超えた分だけ単位あたりの購入費用が割り引きされる.
総量割引(all-units discount): ある一定数量を超えると, 一度に購入したすべての量に対して割引が適用される.
増分割引
いま,発注量 \(Q\) が分岐点 \(\theta\) を超えると, その購入単価が \(c_0\) から \(c_1\) に(\(\theta\) を超えた分だけ)割引されるものとする. 発注の固定費用を \(K\) とし,購入費用の合計を,発注量 \(Q\) の関数として \(c(Q)\) とすると,\(c(Q)\) は
\[ c(Q)= \left\{ \begin{array}{l l} 0 & Q=0 \\ K + c_0 Q & 0 <Q \leq \theta \\ K + c_0 \theta + c_1 (Q-\theta) & \theta <Q \end{array} \right. \] と書くことができる.
総費用は,購入費用と在庫費用の和である. 単位時間あたりの購入費用は,一度に \(Q\) 単位を購入するときにかかる費用 \(c(Q)\) をサイクル時間 \(T\) で割った値であるので, \[ \frac{c(Q)}{T}=\frac{c(Q) d}{Q} \] となる. 在庫費用は,購入費用に対する利子とその他のハンドリング費用や陳腐化費用を分けて考える. 購入費用に対する利子を除いた単位時間・単位数量あたりの在庫保管費用を \(h\) とする. 購入費用のうち,発注固定費用を除いた部分は,\(c(Q)-K\) であるので,単位数量あたりの購入費用は, \((c(Q)-K)/Q\) となる.利子率を \(r\) とすると,単位在庫あたりの金利負担は \(r (c(Q)-K)/Q\) となる. したがって在庫費用は,平均在庫量が \(Q/2\) であることから, \[ \frac{1}{2} ( h + r (c(Q)-K) ) Q \] となる. したがって,単位時間あたりの費用関数 \(f(Q)\) は, \[ f(Q)= \frac{c(Q) d}{Q} + \frac{1}{2} ( h + r (c(Q)-K) ) Q \] となる.
\(Q>0\) としたとき,\(c(Q)\) を以下のように,2本の直線の小さい方をとった関数に変形することができる. \[ c(Q) =\min \left\{ \begin{array}{l} K + c_0 Q \\ K_1 + c_1 Q \end{array} \right. \] ここで,\(K_1=K+(c_0-c_1) \theta\) である.
各直線ごとの問題は,通常の経済発注量モデルと同じ形になるので,最適解を容易に求めることができる.
たとえば,\(c(Q)=K_1+c_1 Q\) の場合には, \[ f(Q)=d c_1 +\frac{d K_1}{Q} + \frac{1}{2} (h +r c_1) Q \] となるので,\(Q\) で微分して \(0\) と置くことによって,最適発注量 \(Q^*_1\) を得ることができる. \[ Q_1^* =\sqrt{ \frac{2 d K_1}{ h+r c_1 } } \] また,最適費用は, \[ f(Q_1^*) = d c_1 + \sqrt{ 2 K_1 d (h+r c_1) } \] である.
同様に,\(c(Q)=K+c_0 Q\) の場合の最適発注量を求め,それを \(Q_0^*\) とする. \[ Q_0^* =\sqrt{ \frac{2 d K}{ h+r c_0 } } \]
\(c_0 >c_1\) であり,かつ \(K <K_1\) であるので,\(Q_0^* <Q_1^*\) となる.
\(c(Q)=K_1+c_1 Q\) と \(c(Q)=K+c_0 Q\) の場合の費用関数は,\(Q=\theta\) で繋がっていることに注意すると, \(f(Q_0^*)\) と \(f(Q_1^*)\) をくらべて小さい方を選択すれば良いことが言える.
一般に,区分 \(j\) に対する購入単価を \(c_j (j=0,1,\ldots,m)\) とすると, \[ Q_j^* = \sqrt{ \frac{2 d K_j}{ h+r c_j } } \] \[ K_j = K+(c_0-c_j) \theta_j \] を区分ごとに計算し,最小費用の区分を求めれば良い.
総量割引
総量割引の場合には,発注量 \(Q\) が分岐点 \(\theta\) を超えると, その購入単価が \(c_0\) から \(c_1\) にすべて割引されるので,購入費用 \(c(Q)\) は, \[ c(Q)= \left\{ \begin{array}{l l} 0 & Q=0 \\ K + c_0 Q & 0 <Q \leq \theta \\ K + c_1 Q & \theta <Q \end{array} \right. \] と書くことができる.
\(c_0 >c_1\) なので, \(c(Q)= K + c_1 Q\) のときの最適発注量 \[ Q_1^* =\sqrt{ \frac{2 d K}{ h+r c_1 } } \] が \(\theta\) 以上のときには,\(Q_1^*\) が最適になる.
\(Q_1^* < \theta\) のときには,\(c(Q)= K + c_0 Q\) のときの最適発注量 \[ Q_0^* =\sqrt{ \frac{2 d K}{ h+r c_0 } } \] と発注量が \(\theta\) のときの総費用をくらべて,小さい方を選択すれば良い.
一般に,区分 \(j\) に対する購入単価を \(c_j (j=0,1,\ldots,m)\) とすると, \[ Q_j^* =\sqrt{ \frac{2 d K}{ h+r c_j } } \] を区分ごとに計算し,それが区分内にある場合には,\(Q_j^*\) を候補とし, 区分外の場合には,分岐点 \(\theta_j\) を候補とすれば良い.
経済発注量モデルを解くための関数 eoq
引数: - K: 発注固定費用 - d: 需要量 - h: 在庫費用(割引モデルの場合には,金利分以外の在庫費用) - b: 品切れ費用; Noneの場合には,品切れを許さないモデルになる. - r: 利子率; 割引モデルの場合に使用する. - c: 割引モデルの場合の区間ごとの割引費用; - theta: 割引モデルの場合の区間の切れ目(分岐点); 最初の区分は必ず0と仮定 - discount:割引の種類を表す文字列を入れる. “incremental”の場合は増量割引, “all”の場合は総量割引, None(既定値)の場合には割引がないモデルになる.
返値: - Q: 最適発注量 - z: 最適値
eoq
eoq (K, d, h, b, r, c, theta, discount=None)
eoq関数の使用例
K = 300.
d = 10.
h = 10.
b = None #40.
r = 0.01
c = [350., 200.]
theta = [0., 30.] #最初の区分は必ず0と仮定
eoq(K, d, h, b, r, c, theta, "incremental")
#eoq(K, d, h, b, r, c, theta)(89.44271909999159, 3073.3126291998988)(Q,R)方策と(s,S)方策のシミュレーションを行う関数 simulate_inventory
\((Q,R)\)方策に基づくを在庫シミュレーションをNumPyを用いて行う。手持ち在庫量に発注済みの量を加えたものを在庫ポジションとよぶ. \((Q,R)\)方策とは,正味在庫ポジション(在庫ポジション \(-\) バックオーダー(品切れ)量)が発注点 \(R\) を下回ったら、固定数量 \(Q\) だけ発注する方策である.
一方, \((s,S)\)方策とは,正味在庫ポジションが発注点 \(s\) を下回ったら, 正味在庫ポジションが \(S\) になるように発注する方策である.
保証リード時間 \(GLT\) と補充リード時間 \(RLT\) に対する \((s,S)\) 方策のシミュレーションは,以下の式に基づく.
- 在庫フロー: \(I_t = I_{t-1} + d_{t-GLT} + Q_{t-RLT}\)
- 正味在庫ポジション: \(NI_t = NI_{t-1} -d_{t}\)
- 発注量 \(Q\): \(NI_t < s\) のとき \(Q_t = [S-NI_t]^+\)
- 正味在庫ポジション (発注後): \(NI_t = NI_{t} + Q_t\)
引数:
- n_samples: シミュレーションを行うサンプル数
- n_periods: 期間数
- mu: 需要の平均(需要は正規分布を仮定する.)
- sigma: 需要の標準偏差
- LT: リード時間
- Q: 発注ロットサイズ
- R: 発注点
- z: 安全在庫係数;安全在庫係数は基在庫レベル \(S\) を求めるときに使われる。
- b: バックオーダー費用
- h: 在庫費用
- fc: 発注固定費用
- S: \((s,S)\)方策のパラメータ; \(s\) は \(R\) と同じ. \(S\) が None(既定値)の場合には, \((Q,R)\) 方策を適用する.
返値:
- cost: 総費用のサンプルごとの期待値を表すNumPy配列で,形状は(n_samples,)
- I: 在庫の時間的な変化を表すNumPy配列で、形状は (n_samples, n_periods+1);在庫の可視化に用いる。
simulate_inventory
simulate_inventory (n_samples=1, n_periods=10, mu=100.0, sigma=10.0, LT=3, Q=300.0, R=100.0, b=100.0, h=1.0, fc=10000.0, S=None)
(Q,R)方策と(s,S)方策による在庫シミュレーション
simulate_inventory関数の使用例
n_samples =1
n_periods =100
alpha = 3.
fc = 0.
mu = 100.
sigma = 6.
b = 100.
h = 2.
LT = 0
from scipy.stats import norm
omega = b/(b+h)
print("臨界率=", omega)
print("安全在庫係数=", norm.ppf(omega) )
z = norm.ppf(omega)
if LT ==0:
s = mu
S = mu
else:
s, S = approximate_ss(mu, sigma, LT-1, b, h, fc) #LT=0には対応していない! LT=1のときが近似公式の0に対応
print(s,S)
# min_Q = Q = np.sqrt(2*fc*mu/h/omega) #EOQ formula
# R = LT*mu + z*sigma*np.sqrt(LT) #z is derived by b and h
# print(Q,R)
cost, I = simulate_inventory(n_samples =n_samples, n_periods =n_periods, mu=mu, sigma=sigma, LT=LT, Q=None, R=s, b=b, h=h, fc=fc, S=S)
#cost.mean(), cost.std()
cost.mean()+alpha*cost.std()臨界率= 0.9803921568627451
安全在庫係数= 2.0619165008094615
100.0 100.00.0plt.plot(I[0]); #在庫の推移の可視化
多段階の場合のシミュレーション
multi_stage_simulate_inventory
multi_stage_simulate_inventory (n_samples=1, n_periods=10, mu=100.0, sigma=10.0, LT=array([1, 1, 1]), s=None, S=None, b=100.0, h=array([10., 5., 2.]), fc=10000.0)
多段階ネットワークに対する(s,S)方策による在庫シミュレーション
# n_samples =1
# n_periods =100
# n_stages = 3
# fc = 1.
# mu = 100.
# sigma = 10.
# b = 100.
# h = np.array([10., 5., 2.])
# LT = np.array([1, 1, 1])
# ELT = np.zeros(n_stages,dtype=int)
# ELT[0] = LT[1]
# for i in range(1,n_stages):
# ELT[i] = ELT[i-1] + 1 + LT[i]
# print("Echelon LT=", ELT)
# s = np.zeros(n_stages)
# S = np.zeros(n_stages)
# for i in range(n_stages):
# s[i], S[i] = approximate_ss(mu, sigma, ELT[i], b, h[i], fc)
# print(s, S)
# for i in range(1):
# cost, I, T = multi_stage_simulate_inventory(n_samples, n_periods, mu, sigma, LT,
# s, S, b =100., h = np.array([10., 5., 2.]), fc=fc)
# print(cost.mean())
# plt.plot(I[0,2]);Echelon LT= [1 3 5]
[218.88226596 433.36782555 650.50643525] [218.88226596 433.36782555 650.50643525]
2800.004477798352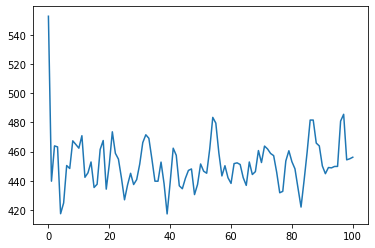
(Q,R)方策のパラメータ最適化関数 optimize_qr
\(Q\) が与えられていないときには, \(Q^*\) は経済発注量モデルを用いて初期化する.
\(Q^*\) を固定し, 発注点 \(R\) は,リード時間内の安全在庫量を初期値として1つずつ増やし,費用が増加した地点を最適な発注点 \(R^*\) とする.
\(R^*\) を固定し, 経済発注量の前後を探索し,費用が増加に転じた点を最適な発注量 \(Q^*\) とする.
期待値だけでなく費用の標準偏差も考慮し, 「期待値 \(+ \alpha\) 標準偏差」 を評価尺度とする.
シミュレーションベースなので,任意の分布,任意の確率過程, 任意の制約に対応できる.
引数:
- n_samples: シミュレーションを行うサンプル数
- n_periods: 期間数
- mu: 需要の平均(需要は正規分布を仮定する.)
- sigma: 需要の標準偏差
- LT: リード時間
- Q: 発注ロットサイズ; Qを固定したいときには整数を入れ,最適化したいときには None を入れる.
- R: 発注点; Rを固定したいときには整数を入れ,最適化したいときには None を入れる.
- z: 安全在庫係数; None(既定値)の場合には,在庫費用とバックオーダー費用から計算される.
- b: バックオーダー費用
- h: 在庫費用
- fc: 発注固定費用
- alpha: リスクの考慮の度合い;「期待値 \(+ \alpha\) 標準偏差」 を評価尺度とする.
返値:
- R: 最適化された発注点
- Q: 最適化された発注量
optimize_qr
optimize_qr (n_samples=1, n_periods=10, mu=100.0, sigma=10.0, LT=3, Q=None, R=None, z=None, b=100.0, h=1.0, fc=10000.0, alpha=1.0)
(Q,R)方策のパラメータ最適化
optimize_qr関数の使用例
# n_samples =100
# n_periods =100
# alpha = 1.
# fc = 10000.
# mu = 100.
# sigma = 10.
# b = 100.
# h = 1.
# LT = 1
# np.random.seed(123)
# R,Q = optimize_qr(n_samples =n_samples, n_periods =n_periods, mu=mu, sigma=sigma, LT=LT, Q=None, R=None, z=z, b=b, h=h, fc=fc, alpha=alpha)
# #print(Q, R)
# #シミュレーションと可視化
# cost, I = simulate_inventory(n_samples =n_samples, n_periods =n_periods, mu=mu, sigma=sigma, LT=LT, Q=Q, R=R, b=b, h=h)
# plt.plot(I[0]); #在庫の推移の可視化
#費用のヒストグラム
plt.hist(cost);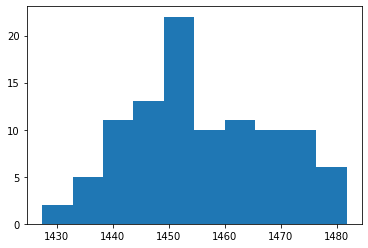
(s,S)方策のパラメータ最適化関数 optimize_ss
\(Q\) が与えられていないときには, \(Q^*\) は経済発注量モデルを用いて初期化する.
\(Q^*\) を固定し, 発注点 \(R=s\) は,リード時間内の安全在庫量を初期値として1つずつ増やし,費用が増加した地点を最適な発注点 \(R^*\) とする.
\(R^*\) を固定し, 「\(R^* +\)経済発注量」の前後を探索し,費用が増加に転じた点を最適な \(S^*\) とする.
期待値だけでなく費用の標準偏差も考慮し, 「期待値 \(+ \alpha\) 標準偏差」 を評価尺度とする.
シミュレーションベースなので,任意の分布,任意の確率過程, 任意の制約に対応できる.
引数:
- n_samples: シミュレーションを行うサンプル数
- n_periods: 期間数
- mu: 需要の平均(需要は正規分布を仮定する.)
- sigma: 需要の標準偏差
- LT: リード時間
- Q: 発注ロットサイズ; Qを固定したいときには整数を入れ,最適化したいときには None を入れる.
- R: 発注点; Rを固定したいときには整数を入れ,最適化したいときには None を入れる.
- z: 安全在庫係数; None(既定値)の場合には,在庫費用とバックオーダー費用から計算される.
- b: バックオーダー費用
- h: 在庫費用
- fc: 発注固定費用
- alpha: リスクの考慮の度合い;「期待値 \(+ \alpha\) 標準偏差」 を評価尺度とする.
- S: 基在庫レベル; 最適化したいときには None(既定値)を入れる.
返値:
- s: 最適化された発注点
- S: 最適化された基在庫レベル
optimize_ss
optimize_ss (n_samples=1, n_periods=10, mu=100.0, sigma=10.0, LT=3, Q=None, R=None, z=None, b=100.0, h=1.0, fc=10000.0, alpha=1.0, S=None)
(s,S)方策のパラメータ最適化
optimize_ss関数の使用例
# n_samples =100
# n_periods =100
# alpha = 1.
# fc = 1.
# mu = 100.
# sigma = 10.
# b = 100.
# h = 10.
# LT = 1
# np.random.seed(123)
# R,S = optimize_ss(n_samples =n_samples, n_periods =n_periods, mu=mu, sigma=sigma, LT=LT, Q=None, R=None, z=z, b=b, h=h, fc=fc, alpha=alpha, S=None)
# s, S = approximate_ss(mu, sigma, LT, b, h, fc)
# print(s, S)
# #シミュレーションと可視化
# for i in range(10):
# cost, I = simulate_inventory(n_samples =n_samples, n_periods =n_periods, mu=mu, sigma=sigma, LT=LT, Q=None, R=R, b=b, h=h, fc=fc, S=S-i)
# print(cost.mean())
# plt.plot(I[0]); #在庫の推移の可視化Use base stock policy!
218.8822659611578 218.8822659611578
763.7424638470262
764.4567798777746
764.5266594870563
765.2828889754412
768.528185341823
770.2273226521506
778.5564569609345
784.1213191908391
788.7634416969585
796.8654287662399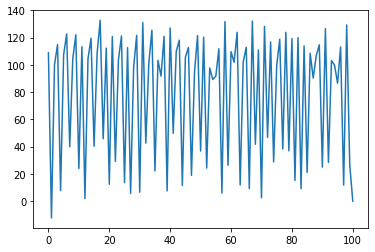
#費用のヒストグラム
# plt.hist(cost);
(s,S)方策の近似最適化関数 approximate_ss
回帰を用いてパラメータを探索した研究に基づく,近似 \(s,S\) の算出
MANAGEMENT SCIENCE Vol. 30, No. 5, May 1984 Printed in U.S.A.
A REVISION OF THE POWER APPROXIMATION FOR COMPUTING (s, S) POLICIES
RICHARDEHRHARDT AND CHARLESMOSIER
we sets = min{sp,S0}a nd S = min{sp + Dp, S0}, where S0 = μL + Φ−1(p/(p + h)) a
引数:
- mu: 需要の平均(需要は正規分布を仮定する.)
- sigma: 需要の標準偏差
- LT: リード時間(0のときに次の期に到着する;シミュレーションのLT=1に相当)
- b: バックオーダー費用
- h: 在庫費用
- fc: 発注固定費用
返値:
- s: 最適化された発注点
- S: 最適化された基在庫レベル
深層学習を用いた拡張が課題となる.
approximate_ss
approximate_ss (mu=100.0, sigma=10.0, LT=0, b=100.0, h=1.0, fc=10000.0)
approximate_ss関数の使用例
# n_samples =1
# n_periods = 100
# fc = 0.
# mu = 100
# sigma = 0
# b = 100.
# h = 1.
# LT = 1
# s, S = approximate_ss(mu, sigma, LT-1, b, h, fc)
# print(s, S)
# #cost, I = simulate_inventory(n_samples =n_samples, n_periods =n_periods, mu=mu, sigma=sigma, LT=LT, Q=None, R=s, b=b, h=h, S=S)
# #plt.plot(I[0]); #在庫の推移の可視化
# #print(cost.mean())99.13000106299978 99.13000106299978# #費用のシミュレーション
# n_samples =100
# n_periods =100
# alpha = 0.
# fc = 10000.
# mu = 100.
# sigma = 10.
# b = 100.
# h = 10.
# LT = 3
# omega = b/(b+h)
# z = norm.ppf(omega)
# print("R=", (LT)*mu+ z*sigma*np.sqrt(LT) )
# R,Q = optimize_qr(n_samples =n_samples, n_periods =n_periods, mu=mu, sigma=sigma, LT=LT, Q=None, R=None, z=z, b=b, h=h, fc=fc, alpha=alpha)
# np.random.seed(123)
# cost, I = simulate_inventory(n_samples =n_samples, n_periods =n_periods, mu=mu, sigma=sigma, LT=LT, Q=Q, R=R, b=b, h=h)
# print("R=",R, "Q=", Q)
# print("RQ-policy cost=", cost.mean())
# s,S = optimize_ss(n_samples =n_samples, n_periods =n_periods, mu=mu, sigma=sigma, LT=LT, Q=None, R=None, z=z, b=b, h=h, fc=fc, alpha=alpha, S=None)
# np.random.seed(123)
# cost, I = simulate_inventory(n_samples =n_samples, n_periods =n_periods, mu=mu, sigma=sigma, LT=LT, Q=None, R=s, b=b, h=h, S=S)
# print("s=",s, "S=", S)
# print("s,S policy cost=", cost.mean())
# #plt.plot(I[0]); #在庫の推移の可視化
# s, S = approximate_ss(mu, sigma, LT, b, h, fc)
# np.random.seed(123)
# cost, I = simulate_inventory(n_samples =n_samples, n_periods =n_periods, mu=mu, sigma=sigma, LT=LT, Q=None, R=s, b=b, h=h, S=S)
# print("s=",s, "S=", S)
# print("Approximate s,S policy cost=", cost.mean())
# plt.plot(I[0]); #在庫の推移の可視化R= 323.12595676092786
R= 323 Q= 461
RQ-policy cost= 4714.398125108141
s= 313 S= 772
s,S policy cost= 4686.765178752777
s= 349.55651923599106 S= 768.2721946765712
Approximate s,S policy cost= 4855.83862088315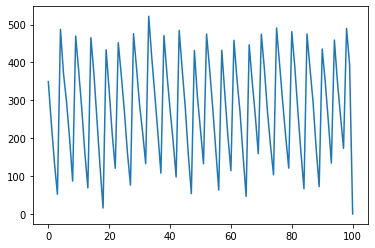
多段階への拡張
\(Q^*\) が決まっている場合: サイクル時間 \(CT = Q^*/\mu\) を計算し, \(L= \max \{ CT, LT \}\) をリード時間 \(L\) として最適な基在庫レベル \(S^*\) を定期発注方策最適化で求める. \(L\)分の平均在庫量 \(L \mu\) を減じて安全在庫量を求め, さらにリード時間分の平均需要量 \(\mu LT\) を加えたものが発注点 \(R^*\) となる.
\(Q^*\) を最適化した場合: 定期発注方策最適化で求めた \(R^*\) を固定し, 最適な発注量 \(Q^*\) を地点ごとに(上の関数optimize_qrを用いて)再最適化し,これを繰り返す.
多段階の \((Q,R)\)方策と \((s,S)\) 方策のシミュレータを作り, パラメータの調整を行う.
(s,S)方策の最適パラメータの可視化
# fc = 10000.
# mu = 100.
# sigma = 10.
# b = 1000.
# h = 10.
# LT = 3
# s, S = approximate_ss(mu, sigma, LT, b, h, fc)
# print(s, S)398.3997427604041 817.1154180141727# hlist, slist, Slist = [], [], []
# Rlist, Qlist =[],[]
# for h in range(1,1000, 1):
# hlist.append(h)
# s, S = approximate_ss(mu, sigma, LT, b, h, fc)
# #s,S = optimize_ss(n_samples =n_samples, n_periods =n_periods, mu=mu, sigma=sigma, LT=LT, Q=None, R=None, z=z, b=b, h=h, fc=fc, alpha=alpha, S=None)
# slist.append(s)
# Slist.append(S)
# omega = b/(b+h)
# z = norm.ppf(omega)
# R = (LT+1)*mu+ z*sigma*np.sqrt(LT+1)
# Rlist.append(R)
# Qlist.append(s+np.sqrt(2*fc*mu/h/omega))
# plt.plot(hlist,slist);
# plt.plot(hlist,Slist);
# #plt.plot(hlist,Rlist);
# #plt.plot(hlist,Qlist);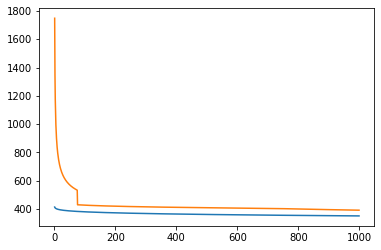
定期発注方策(単一段階モデル)
#hide
ここでは,発注を行うことができるタイミングが限定されている定期発注方策を考える. 定期発注方策では,時間を離散値として取り扱う.実際には,日単位などで在庫を管理することが多いため, 定期発注方策は,多くの実際問題で適用可能なモデルである. 時間は,期とよばれる単位に分割されており,期を \(1,2,\ldots,t,\ldots,t_{\max}\) と記す.
はじめに,1つの小売店に顧客が需要を引き起こす場合を考える.
モデルに必要な記号を導入する.
\(D_t\): \(t\) 期における需要量.任意の分布もしくは確率過程. ここでは,シミュレーションを行いながら,基在庫レベルを最適化するので,シミュレーション可能な任意の 需要を仮定して良い.
\(L\): リード時間(lead time);\(t\) 期の期末に発注された商品は,\(t+L+1\) 期の期首に 到着するものと仮定する.この発注から到着の間の時間差をリード時間とよぶ.
\(s\): 基在庫レベル. 各期の期末に,期末在庫ポジションが基在庫レベル \(s\) になるように,上流の在庫地点に対して,発注するものとする. 期首から期末にかけて需要 \(D_{t}\) が発生し,その後で発注するものと仮定する.
\(c\): 発注量の上限.容量ともよばれる.
\(q_t\): \(t\) 期における発注量. \(t\) 期の期末に,期末の在庫ポジション(在庫量に輸送中在庫量を加えたもの)\(I_{t}-D_t + T_{t}\) が基在庫レベル \(s\) になるように発注するものとする.ただし,発注量の上限を超えた場合には, 上限いっぱいの量を発注するものとする. これを式で表すと,以下のようになる.
\[ q_t = \min \left\{ c, [ s- (I_{t}-D_t + T_{t})]^+ \right\} \]
ここで,\([ \cdot ]^+\) は,\(\max \{0, \cdot\}\) を表す記号である.
- \(I_t\): \(t\) 期の期首における正味在庫量;期首に以前注文した量を受け取った後の在庫量で測定するものとする. なお,正味在庫量は,「実在庫量 \(-\) バックオーダー(品切れ)量」を表す, したがって,\(t+1\) 期の期首在庫量 \(I_{t+1}\) は,\(t\) 期の期首在庫量 \(I_t\) から需要量 \(D_t\) を減じた後, \(t+1\)期の期首に \(t-L\) 期に発注された量 \(q_{t-L}\) を受け取るので, 在庫量と需要量,発注量の関係式(在庫フロー保存式)は,以下のようになる.
\[ I_{t+1} =I_{t} -D_{t} +q_{t-L} \]
- \(T_t\): \(t\) 期の期首における輸送中在庫量; 在庫量と同様に,以前注文した量を受け取った後で測定するものとする. \(t+1\) 期の期首の輸送中在庫量は,前の期の輸送中在庫量 \(T_t\) に,新たに発注した量 \(q_t\) を加え, \(t+1\) 期の期首に到着する量 \(q_{t-L}\) を減じるので,以下のように計算できる.
\[ T_{t+1} =T_{t} + q_{t} - q_{t-L} \]
\(b\): 単位期間,単位バックオーダー量あたりの品切れ費用.
\(h\): 単位期間,単位在庫量あたりの在庫保管費用.
\(t\) 期の費用を表す確率変数 \(C_t\) は,期首における(過去の注文を受け取った後の)正味在庫量で測定するものと仮定すると,
\[ C_t = b [I_t]^- + h [I_t]^+ \]
と書くことができる.
目的関数は,\(t_{\max}\) 期の期待費用 \[ \frac{1}{ t_{\max} } \sum_{t=1}^{t_{\max}} \mathbf{E}[ C_t ] \]
であり,これを最小化する.
ここで,モデルの仮定に関する注意を述べておく. 期中に需要が発生し,期首に(注文を受け取った後で)在庫を評価すると仮定していたので, 期首の在庫が \(0\) でも品切れが生じないことになる(期中に予約をして,翌日の朝に受け取ると解釈もできるが, 多少無理がある). また,発注を行うタイミングも,実際には期末でなく,期中に行われることが多い. たとえば,あるスーパーでは, 午前中の暇な時間帯に(POSシステムがあるにも関わらず)実在庫を調べ,発注を行っている. ここで行ったモデルの仮定は,記号の簡潔さと従来の研究との整合性のためであり, 実際にはシミュレーションを行いながら,パラメータの最適化を行うので,ほとんどの現実問題に対処可能である.
変数は基在庫レベル \(s\) である. 目的関数の \(s\) による微分値 \((I_t)'\) は、単一段階、モデルにおいてはすべて \(1\) になるので、 \(t\) 期の費用関数 \(C_t\) の \(s\) による微分は,
\[ (C_t)' = -b (I_t)' \mathbf{1}[I_t<0] + h(I_t)' \mathbf{1}[I_t>0] \]
となる.
また,目的関数(\(C_t\) の期待値)の \(s\) による微分は,確率 \(1\) で微分値の期待値
\[ \mathbf{E}\left[ \frac{1}{t_{\max}} \sum_{t=1}^{t_{\max} } (C_t)' \right] \]
に収束することが示される. したがって,\((C_t)'\) の期待値をとり,これが負ならば基在庫レベル \(s\) を増やし,正ならば減らせば良いことが分かる.
実際には,非線形計画による探索を行う必要があるが,通常の(微分値のみを利用した比較的単純な)非線形最適化の手法が適用できる.
上のアルゴリズムを実装したものが、以下のbase_stock_simulationである。
引数:
- n_samples: シミュレーションを行うサンプル数
- n_periods: 期間数
- demand: 需要のサンプルを表すNumPyの配列で、形状は (n_samples, n_periods)。
- capacity: 容量(生産量上限)
- LT: リード時間
- b: バックオーダー費用
- h: 在庫費用
- S: 基在庫レベル
返値:
- dC: 各地点における総費用の基準在庫レベルによる微分の期待値
- total_cost: 総費用の期待値
- I: 在庫の時間的な変化を表すNumPy配列で、形状は (n_samples, n_periods+1)。
#hide ““” Solve the base-stock level optimization problem using the simulation based approach (infinitestimal perterbation analysis: IPA)
The algorithm is based on:
@article{Glasserman1995,
author={P. Glasserman and S. Tayur},
title={Sensitivity Analysis for Base Stock Levels in Multi-Echelon Production-Inventory Systems},
journal={Management Science},
year={1995},
volume={41},
pages={263--281},
annote={ }
}““”
base_stock_simulation
base_stock_simulation (n_samples, n_periods, demand, capacity, LT, b, h, S)
単一段階在庫システムの定期発注方策に対するシミュレーションと微分値の計算
base_stock_simulation_using_dist
base_stock_simulation_using_dist (n_samples, n_periods, demand, capacity, LT, b, h, S)
単一段階在庫システムの定期発注方策に対するシミュレーションと微分値の計算
# n_samples = 10
# n_periods = 1000
# capacity = 10.
# convergence = 1e-5
# b = 100
# h = 1
# LT = 1
# critical_ratio = b/(b+h)
# S = best_dist.ppf(critical_ratio) + 5
# print(S, best_dist.ppf(0.01))
# demand = best_dist.rvs((n_samples,n_periods)) + 5.# print("t: S dS Cost")
# for iter_ in range(100):
# dC, cost, I = base_stock_simulation_using_dist(n_samples, n_periods, demand, capacity, LT, b, h, S)
# S = S - 0.1*dC
# print(f"{iter_}: {S:.2f} {dC:.3f} {cost:.2f}")
# if dC**2<=convergence:
# breakbase_stock_simulation関数を利用した在庫最適化
上で作成した関数を用いて、最適化を行う。base_stock_simulationは、微分値を返すので、最急降下法を適用して最適値を探索する。 微分値の2乗がepsilonを下回ったら終了する。
#(Q,R)方策と同じ仮定で実験
n_samples =100
n_periods =100
alpha = 1.
fc = 10000.
mu = 100.
sigma = 10.
b = 100.
h = 10.
LT = 3
np.random.seed(123)
from scipy.stats import norm
omega = b/(b+h)
print("臨界率=", omega)
print("安全在庫係数=", norm.ppf(omega) )
z = norm.ppf(omega)
capacity = np.inf
S = mu*LT + z*sigma*np.sqrt(LT)
convergence = 1e-5
print("Initial S=", S)
demand = np.random.normal(mu, sigma, (n_samples, n_periods))
print("t: S dS Cost")
for iter_ in range(100):
dC, cost, I = base_stock_simulation(n_samples, n_periods, demand, capacity, LT, b, h, S)
S = S - 1.*dC
print(f"{iter_}: {S:.2f} {dC:.3f} {cost:.2f}")
if dC**2<=convergence:
break臨界率= 0.9090909090909091
安全在庫係数= 1.3351777361189363
Initial S= 323.12595676092786
t: S dS Cost
0: 323.56 -0.439 377.45
1: 323.51 0.056 377.35
2: 323.52 -0.010 377.35
3: 323.53 -0.010 377.35
4: 323.52 0.012 377.35
5: 323.53 -0.010 377.35
6: 323.53 0.001 377.35n_samples = 100
n_periods = 10000
mu = 100
sigma = 10
LT = 3
z = 2.43
b, h = 100, 1
capacity = 1000.
S = mu*LT + z*sigma*np.sqrt(LT)
convergence = 1e-5
print("Initial S=", S)
demand = np.random.normal(mu, sigma, (n_samples, n_periods))
print("t: S dS Cost")
for iter_ in range(100):
dC, cost, I = base_stock_simulation(n_samples, n_periods, demand, capacity, LT, b, h, S)
S = S - 1.*dC
print(f"{iter_}: {S:.2f} {dC:.3f} {cost:.2f}")
if dC**2<=convergence:
breakInitial S= 342.08883462392373
t: S dS Cost
0: 341.86 0.228 46.55
1: 341.66 0.200 46.50
2: 341.49 0.175 46.47
3: 341.33 0.153 46.44
4: 341.20 0.133 46.42
5: 341.09 0.114 46.40
6: 340.99 0.098 46.39
7: 340.90 0.086 46.38
8: 340.83 0.073 46.37
9: 340.77 0.062 46.37
10: 340.71 0.053 46.36
11: 340.67 0.046 46.36
12: 340.63 0.039 46.36
13: 340.59 0.033 46.36
14: 340.57 0.029 46.36
15: 340.54 0.024 46.36
16: 340.52 0.021 46.35
17: 340.50 0.018 46.35
18: 340.49 0.015 46.35
19: 340.47 0.012 46.35
20: 340.46 0.011 46.35
21: 340.46 0.008 46.35
22: 340.45 0.007 46.35
23: 340.44 0.006 46.35
24: 340.44 0.005 46.35
25: 340.43 0.004 46.35
26: 340.43 0.004 46.35
27: 340.43 0.003 46.35plt.plot(I[0,:1000]);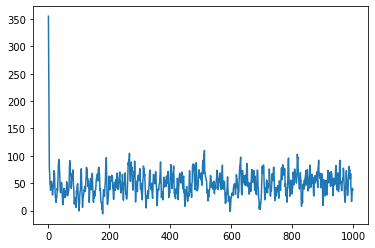
定期発注方策(多段階在庫モデル)
#hide
ここでは,単一段階モデルを直列多段階の場合に拡張する. この結果は,Glasserman―Tayur に基づく. 多くの実際問題は,直列多段階に分解して考えることができるので,このモデルは実務的にも有意義であるが, 以下で解説する一般のネットワークに対する基礎を与えるという意味でも重要である.
点の順番は下流(需要地点側)から \(0,1,\ldots,n-1\) と並んでいるものとし, \(n\) 番目には,点 \(n-1\) に品目を供給する外部の点があるものと仮定する. この \(n\) 番目の点には十分な在庫があり,品切れはしないものとする.
多段階の問題では,基在庫レベルのかわりに,エシェロン基在庫レベルを用いる. 各段階におけるエシェロン在庫ポジションが,エシェロン基在庫レベルより小さいときには, エシェロン基在庫レベルになるように,上流の地点に発注を行う. この方策を,エシェロン基在庫方策とよぶ.
直列に並んだ在庫地点を段階とよび,下流から数えて \(i\) 番目の在庫地点を,第 \(i\) 段階とよぶ. 単一段階のときの記号に, 上添字 \(i\) をつけたものを,多段階用の記号とする. たとえば,第 \(i\) 段階の \(t\) 期における正味在庫量は, \(I_t^i\) と記す.
この記号を用いると,エシェロン基在庫方策は,エシェロン基在庫レベル \(s^i\) を与えたとき, 期末のエシェロン在庫ポジション \[ \sum_{j=0}^i (I_t^j +T_t^j) -D_t \] を \(s_i\) にするように発注を行う方策と定義できる.
実際には,発注量の上限(容量)\(c_i\) と上流の在庫地点の在庫量 \(I_t^{i+1}\) によっても制限を受けるので, 発注量 \(q_t^i\) は,
\[ q^i_t = \min \left\{ c_i, \left[ s^i + D_t- \sum_{j=1}^i (I^j_{t} + T^j_{t}) \right]^+, [ I_t^{i+1}]^+ \right\} \]
となる.ただし,\(i=n-1\) のときには,\(I_t^{i+1}\) を除く.
正味在庫と輸送中在庫の再帰式は,それぞれ
\[ I^i_{t+1} =I^i_{t} -q^{i-1}_{t} +q^i_{t-L_i} \]
\[ T^i_{t+1} =T^i_{t} + q^i_{t} - q^i_{t-L_i} \]
となる. ただし,\(i=0\) のときには,上式における, 上流の地点からの発注量 \(q^{i-1}_{t}\) は需要量 \(D_t\) に置き換える.
初期条件は,在庫量については \(I^0_0=s^0\), \(I^i_0=s^i-s^{i-1}, i=1,2,\ldots,n-1\) と設定し, その他の変数については,すべて \(0\) と設定する.
\(t\)期の費用を表す確率変数 \(C_t\) は,
\[ C_t = b [I^0_t]^- + h^0 [I^0_t]^+ + h^0 T_t^0 +\sum_{j=1}^{n-1} h^j (I^j_t +T^{j}_t) \]
と書くことができる. ここで, \(b\) は品切れ費用であり,最終需要地点(点\(0\))でのみ課せられるものとする. \(h^i\) は \(i\)段階の在庫費用である(エシェロン在庫費用でないことに注意されたい). また,ここでは,輸送中在庫量に対する在庫費用は,下流の在庫地点の在庫費用で計算するものと仮定している.
目的関数は,\(t_{\max}\) 期の期待費用
\[ \frac{1}{t_{\max}} \sum_{t=1}^{t_{\max}} \mathbf{E}[ C_t ] \]
であり,これを最小化する.
変数は基在庫レベル \(s^i,i=0,1,\ldots,n-1\) である.シミュレーションをしながら, 目的関数の各 \(i (=i^*)\) に対する \(s^i (=s^*)\) による微分値の期待値を計算する.
生産量計算式の微分は,以下のような場合分けを必要とする.
\[ \frac{d q^i_t}{d s^*} = \left\{ \begin{array}{l l } 0 & 容量制約が制約のとき \\ 0 & 発注量が 0 のとき \\ (I_t^{i+1})' & i+1 番目の地点の在庫が制約のとき \\ \mathbf{1}[ i=i^*] - \sum_{j=0}^i \left( \frac{d I^j_{t}}{d s^*} +\frac{d T^j_{t}}{d s^*} \right) & それ以外 \end{array} \right. \]
在庫フロー保存式を \(s^*\) で微分すると,
\[ \frac{d I^i_{t+1}}{d s^*} = \frac{d I^i_{t}}{d s^*} - \frac{d q^{i-1}_t}{d s^*} + \frac{d q^i_{t-L_i}}{d s^*} \]
となる.ただし,\(i=0\) のときには,右辺の第\(2\)項目 \(d q^{i-1}_t/d s^*\) は除くものとする.
同様に,輸送中在庫の計算式を \(s^*\) で微分すると,
\[ \frac{d T^i_{t+1}}{d s^*} = \frac{d T^i_{t}}{d s^*} + \frac{d q^i_{t}}{d s^*} - \frac{d q^i_{t-L_i}}{d s^*} \]
となる.
上の再帰式を使うと,微分値をシミュレーションをしながら順次更新していくことができる. 在庫量の微分値の初期値は,在庫量の初期値の設定から、 \[(I^0_0)'=\mathbf{1}[ i^*=0], \] \[(I_0^i)'= \mathbf{1}[ i^*=i] - \mathbf{1}[ i^*=i-1 ], i=1,\cdots,n-1\] となる. 他の変数の微分値は,すべて \(0\) である.
\(t\) 期の費用関数 \(C_t\) の \(s^*\) による微分は,
\[ (C_t)' = -b (I^0_t)' \mathbf{1}[ I^0_t<0] + h_0 (I^0_t)' \mathbf{1}[ I^0_t>0 ] + h_0 (T_t^0)' +\sum_{i=1}^{n-1} h_i \left\{ (T^i_t)' +(I^{i-1}_t)' \right \} \]
となる.
目的関数(\(C_t\) の期待値)の \(s^*\) による微分は,確率 \(1\) で微分値の期待値
\[ \mathbf{E}\left[ \frac{1}{t_{\max}} \sum_{t=1}^{t_{\max}} (C_t)' \right] \]
に収束するので,\((C_t)'\) の期待値をもとに,\(s^*\) の更新を行う.
上のアルゴリズムを実装したものが、以下のmulti_stage_base_stock_simulationである。
多段階在庫システムの定期発注方策に対するシミュレーションと微分値の計算関数 multi_stage_base_stock_simulation
多段階在庫システム対して実装したものが、multi_stage_base_stock_simulationである。
引数:
- n_samples: シミュレーションを行うサンプル数
- n_periods: 期間数
- demand: 需要地点ごとの需要量を保持した辞書。キーは顧客の番号。値は、需要のサンプルを表すNumPyの配列で、形状は (n_samples, n_periods)。
- capacity: 容量(生産量上限)を表すNumPy配列
- LT: 地点毎のリード時間を表すNumPy配列
- b: バックオーダー費用
- h: 在庫費用
- S: 基在庫レベル
返値:
- dC: 各地点における総費用の基準在庫レベルによる微分の期待値
- total_cost: 総費用の期待値
- I: 在庫の時間的な変化を表すNumPy配列で、形状はグラフの点の数をn_stagesとしたとき (n_samples, n_stages, n_periods+1)。
multi_stage_base_stock_simulation
multi_stage_base_stock_simulation (n_samples, n_periods, demand, capacity, LT, b, h, S)
多段階在庫システムの定期発注方策に対するシミュレーションと微分値の計算
multi_stage_base_stock_simulation関数を利用した在庫最適化
上で作成した関数を用いて、最適化を行う。multi_stage_base_stock_simulationは、微分値を返すので、最急降下法を適用して最適値を探索する。 微分値の2乗和がepsilonを下回ったら終了する。
# 多段階 基在庫レベル方策 在庫シミュレーション
np.random.seed(123)
n_samples = 10
n_stages = 3
n_periods = 1000
mu = 100
sigma = 10
LT = np.array([1, 1, 1])
# 初期エシェロン在庫量は、最終需要地点以外には、定期発注方策の1日分の時間を加えておく。
# ELT = LT.cumsum()
# ELT = ELT + 1
# ELT[0] = ELT[0]-1
# ELT[2]+=1
ELT = np.zeros(n_stages)
ELT[0] = LT[1]
for i in range(1,n_stages):
ELT[i] = ELT[i-1] + 1 + LT[i]
print("Echelon LT=", ELT)
z = 1.33
b = 100
h = np.array([10., 5., 2.])
S = mu*(ELT) + z*sigma*np.sqrt(ELT)
print("S=", S)
capacity = np.array([120., 120., 130.])
demand=np.random.normal(mu, sigma, (n_samples, n_periods))
print("t: Cost |dC| S ")
epsilon=0.01
for iter_ in range(100):
dC, cost, I=multi_stage_base_stock_simulation(n_samples, n_periods, demand, capacity, LT, b, h, S)
sum_=0.
for j in range(n_stages):
sum_ += dC[j]**2
S[j]=S[j] - 1.*dC[j]
print(f"{iter_}: {cost:.2f}, {sum_:.3f}", S)
if sum_ <= epsilon:
breakEchelon LT= [1. 3. 5.]
S= [113.3 323.03627574 529.7397041 ]
t: Cost |dC| S
0: 2757.29, 92.626 [112.3865 326.23927574 538.7692041 ]
1: 2733.44, 27.943 [113.318 329.28117574 542.9908041 ]
2: 2724.89, 9.334 [113.6215 331.12797574 545.4055041 ]
3: 2724.59, 4.356 [114.0775 332.28437574 547.0821041 ]
4: 2724.66, 2.075 [114.235 333.08457574 548.2694041 ]
5: 2725.86, 1.013 [114.33 333.64117574 549.1028041 ]
6: 2726.98, 0.687 [114.3505 334.09137574 549.7981041 ]
7: 2728.21, 0.347 [114.434 334.44877574 550.2592041 ]
8: 2728.95, 0.186 [114.5095 334.67267574 550.6198041 ]
9: 2729.49, 0.102 [114.531 334.81887574 550.9031041 ]
10: 2730.01, 0.085 [114.5225 334.95277574 551.1627041 ]
11: 2730.59, 0.049 [114.592 335.01267574 551.3633041 ]
12: 2730.75, 0.041 [114.6175 335.05577574 551.5587041 ]
13: 2731.03, 0.034 [114.6415 335.06957574 551.7409041 ]
14: 2731.26, 0.029 [114.6415 335.07687574 551.9096041 ]
15: 2731.54, 0.021 [114.6275 335.10497574 552.0495041 ]
16: 2731.84, 0.009 [114.6635 335.13047574 552.1310041 ]#hide ### Adamによる最適化
深層学習で定番のAdamで最適化をしてみたが、収束は悪い。
#可視化(最初のサンプルを表示)
# from plotly.subplots import make_subplots
# fig = make_subplots(rows=3, cols=1, subplot_titles= ["Stage " + str(i) for i in range(3)] )
# for j in range(3):
# trace = go.Scatter(
# x= list(range(n_periods)),
# y= I[0,j,:],
# mode = 'markers + lines',
# marker= dict(size= 5,
# line= dict(width=1),
# opacity= 0.3
# ),
# name ="Stage "+str(j)
# )
# fig.add_trace(
# trace,
# row=j+1, col=1
# )
# fig.update_layout(height=1000,title_text=f"Inventories for all stages", showlegend=False)
# plotly.offline.plot(fig)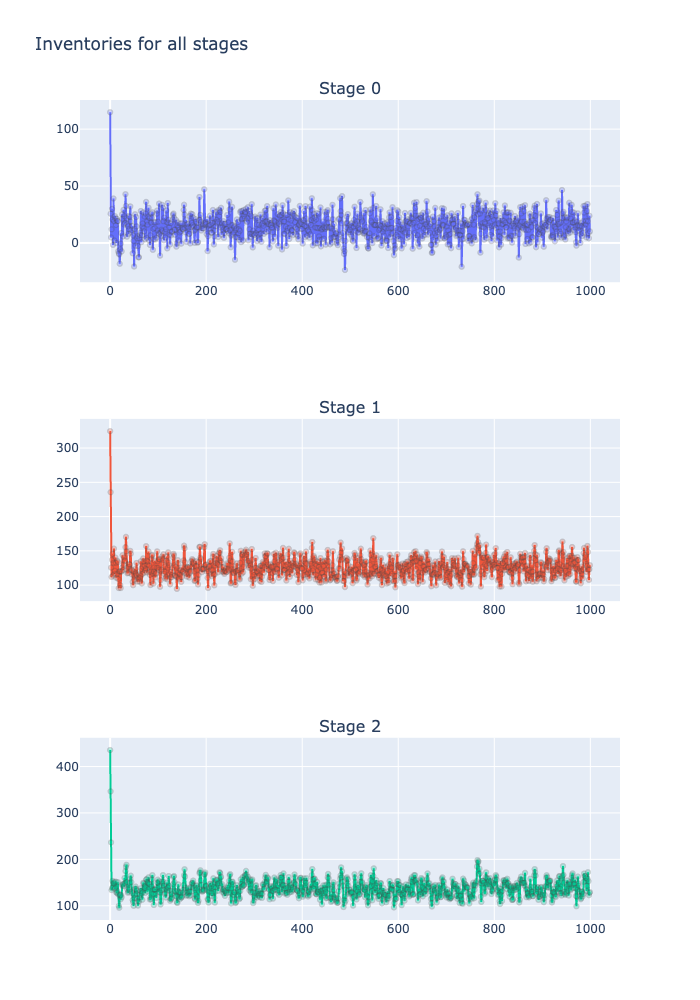
定期発注方策(一般ネットワークモデル)
#hide
実際には,組立工程があったり,複数の地点から発注を受けたるする場合がある. 以下では,一般のネットワークの場合に,上の手法を拡張することを考える.
ある地点 \(i\) が複数の地点から発注を受け,さらにその地点自身でも需要が発生する場合を考える. すべての需要(発注)に応えるだけの在庫量がない場合に, 複数の需要(発注)に対して,どのように在庫を割り振るかを決める必要がある. これを分配ルール(allocation rule)とよぶ. 代表的な分配ルールには,以下のものがある.
- 優先順位法: 直接需要ならびに(複数の)下流の在庫地点に対して,優先順位を付けておき,その順に需要(発注)量を満たす.
- 発注量比例配分法: 需要(発注)量に応じて比例配分をする. この方法だと,供給配分に起因する鞭効果が発生し,安全在庫量が増えてしまう危険性がある.
- 実績比例配分法: 過去の実績に応じて,在庫の比例配分を行う.この方法だと,ある顧客の過去の実績が多く,かつ今回の発注分が少ない場合に,過剰な配分をしてしまい,(この顧客用に確保された)在庫が残っているにもかかわらず,他の顧客の需要を満たすことができないという理不尽な現象が起きる危険性がある.
- 最適配分法: 線形計画問題を解くことによって,過去の実績から計算された優先度と配分量の積の合計を最大化するように配分する.
以下では,実績比例配分法を例として解説する.
ネットワークを表現するための記号を導入しておく.
\(PARENT_i\): ネットワークにおける点 \(i\) の直後の点の集合であり,点 \(i\) が直接供給を行う地点の集合を表す.
\(ANCESTOR_{i}\): 点 \(i\) からネットワークの有向枝を辿って到達可能な点に対応する点集合. 点 \(i\) 自身も含めた点集合と定義する.
\(CHILD_i\): ネットワークにおける点 \(i\) の直前の点の集合であり,点 \(i\) が発注を行う点の集合を表す。 \(CHILD_i\) に発注したすべての部品が揃わないと生産できないものと仮定する。
\(\phi_{ij}\): 点 \(j\) に対応する品目を \(1\)単位製造するために必要な点 \(i\) の品目の量. これは,ネットワークが部品展開表を表すときに用いられるパラメータであり,親品目 \(j\) を製造するために必要 な子品目 \(i\) の量を,枝 \((i,j)\) に付加したものである. 品目の量を表す単位として,\(i\)-unit,\(j\)-unitを導入しておくと分かりやすい. ちなみに,\(\phi_{ij}\) の単位(次元)は,\([ i\)-units \(/\) \(j\)-unit \(]\) である.
上流の地点が存在しない,言い換えれば \(CHILD_i\) が空の点に対しては,その上流の地点に十分な 在庫があるものとし,品切れはしないものとする.
\(t\) 期の期首在庫量が与えられている状態で,需要が発生する.需要はすべての点で発生する可能性があるものとする. (つまり,部品に対しても需要があるものと仮定する.)点 \(i\) における \(t\)期の需要を \(D_t^i\) と記す. 期末に,割当ルールによって,下流の地点に対する在庫の配分を行い, 次いで発注量を決定する.これによって,次期の期首在庫 \(I_{t+1}^i\) が定まる.
在庫地点 \(i\) の在庫地点の \(t\) 期における正味在庫量を \(I_t^i\) と記す. この記号を用いると,エシェロン基在庫方策は,エシェロン基在庫レベル \(s^i\) を与えたとき, \(t\) 期末のエシェロン在庫ポジション \[ E_i^t = \sum_{j \in ANCESTOR_i } \rho_{ij} ( I_t^j +T_t^j -D_t^j ) \] を \(s_i\) にするように発注を行う方策と定義できる.
複数の下流の在庫地点からの注文に対して, 現在の在庫で対応できない場合には,過去の実績に応じて,比例配分を行うものとする.
在庫地点 \(i\) の在庫を下流の在庫地点 \(j\) の配分するときの比率(配分比)を \(\alpha_{ij}\) とする. また,在庫地点 \(i\) が直接の需要 \(D_t^i\) を持っている場合には, その需要に対する配分比を \(\alpha_{i0}\) とする.
配分比は, \[ \alpha_{i0}+ \sum_{j \in PARENT_i} \alpha_{ij} =1 \] を満たすように設定する.
発注量の上限(容量)\(c_i\) と上流の在庫地点の在庫量によっても制限を受けるので, 発注量 \(q_t^i\) は, \[ q_t^i =\min \left\{ \begin{array}{l } c_i \\ \left[ s_i - E_t^i \right]^+ \\ \min_{k \in CHILD_i} \alpha_{ki} [ I_t^k ]^+ /\phi_{ki} \end{array} \right. \] と決められる.
正味在庫量の計算は, \[ I_{t+1}^i = I_{t}^i - \sum_{j \in PARENT_i} \phi_{ij} q_t^j - D_t^i +q_{t-L_i}^i \] と行う.
最後に輸送中在庫量は, \[ T_{t+1}^i =T_{t}^i +q_{t}^i -q_{t-L_i}^i \] と更新する.
変数の初期値は,在庫量については, \[ I_0^i =s^i -\sum_{j \in PARENT_i} \phi_{ij} s^j \] と設定し,その他の変数は,すべて \(0\) に設定する.
\(t\) 期の費用を表す確率変数 \(C_t\) は, \[ C_t = \sum_{i=1}^n b^i [ I^i_{t} ]^- + \sum_{i=1}^n h^i \left\{ [I^i_t]^+ + T^{i}_t \right\} \] と書くことができる. ここで,\(b^i\) は,点 \(i\) に対する直接需要の品切れ費用であり, \(h^i\) は \(i\) 段階の在庫費用である. また,輸送中在庫量に対する在庫費用は,下流の在庫地点の在庫費用で計算するものと仮定している.
微分値の計算は,直列多段階の場合と同様に,以下のようになる.
実績比例配分法の場合には,発注量の微分値の更新式は, \[ \frac{d q^i_t}{d s^*} = \left\{ \begin{array}{l l } 0 & 容量制約が制約のとき \\ 0 & 発注量が 0 のとき \\ \alpha_{ki} (I_t^{k})' & 上流の点 k の在庫が制約のとき \\ \mathbf{1}[ i=i^*] - \sum_{j \in ANCESTOR_j } \rho_{ij} \left( \frac{d I^j_{t}}{d s^*} +\frac{d T^j_{t}}{d s^*} \right) & それ以外 \end{array} \right. \] となる.
在庫の微分値の更新式は,
\[ \frac{d I^i_{t+1}}{d s^*} = \frac{d I^i_{t}}{d s^*} - \sum_{j \in PARENT_i} \phi_{ij} \frac{d q^{j}_t}{d s^*} + \frac{d q^i_{t-L_i}}{d s^*} \] となる.
最後に,輸送中在庫量の更新式は,直列の場合と同様に, \[ \frac{d T^i_{t+1}}{d s^*} = \frac{d T^i_{t}}{d s^*} + \frac{d q^i_{t}}{d s^*} - \frac{d q^i_{t-L_i}}{d s^*} \] となる.
各点 \(i\) の在庫量の,点 \(i^*\) のエシェロン基在庫レベル \(s^*\) による微分値の初期値は, \[ \frac{d I_0^i}{d s^*} = \mathbf{1} [i=i^*] -\sum_{j \in PARENT_i} \phi_{ij} \mathbf{1}[ j=i^*] \] と設定し,その他の変数の微分値は,すべて \(0\) に設定する.
\(t\) 期の費用関数 \(C_t\) の \(s^*\) による微分は,
\[ (C_t)' = - \sum_{i=1}^n b^i (I^i_t)' \mathbf{1}[I^i_t <0] + \sum_{i=1}^n h^i \left\{ (I^i_t)' \mathbf{1}[ I^i_t>0 ] + (T^i_t)' \right \} \]
となる.
前節までと同様に, 目的関数(\(C_t\) の期待値)の \(s^*\) による微分は,確率 \(1\) で微分値の期待値 に収束するので,\((C_t)'\) の期待値をもとに,\(s^*\) の更新をする非線形最適化を行う.
また,収束には時間がかかるので,良い初期解から出発することが肝要である. ここでは,各点上での生産時間を \(1\) 期(日)としたときの点 \(i\) におけるエシェロンリード時間 \(ELT_i\), 累積需要の標準偏差(の推定値) \(\sigma_i\),安全在庫係数の推定値 \(z_i\) を用いて,以下のように決めるものとする.
\[ (ELT_i-1) \left( \sum_{j \in ANCESTOR_i } \rho_{ij} D^j \right) + \sigma_i z_i \sqrt{ELT_i-1} \]
ここで,エシェロンリード時間から \(1\) 期(日)を減じるのは, 需要地点以外の下流の地点をもつ在庫地点では,在庫量が \(0\) だと,下流の地点の生産ができないので, 必ず一定量の在庫をもつ必要があるが,最終需要地点における在庫は \(0\) に近づけるようにするためである.
ネットワーク型定期発注方策に対するシミュレーションと微分値の計算関数 network_base_stock_simulation
一般のネットワークに対して実装したものが、以下のnetwork_base_stock_simulationである。
引数:
- G: 有向グラフ(SCMGraphのインスタンス)
- n_samples: シミュレーションを行うサンプル数
- n_periods: 期間数
- demand: 需要地点ごとの需要量を保持した辞書。キーは顧客の番号。値は、需要のサンプルを表すNumPyの配列で、形状は (n_samples, n_periods)。
- capacity: 容量(生産量上限)を表すNumPy配列
- LT: 地点毎のリード時間を表すNumPy配列
- ELT: 地点毎のエシェロンリード時間を表すNumPy配列
- b: バックオーダー費用
- h: 在庫費用
- S: 基在庫レベル
- phi: 部品展開表における親製品を製造するために必要な子製品の量
- alpha: 上流の在庫地点が下流の在庫地点に在庫を配分する率
返値:
- dC: 各地点における総費用の基準在庫レベルによる微分の期待値
- total_cost: 総費用の期待値
- I: 在庫の時間的な変化を表すNumPy配列で、形状はグラフの点の数をn_stagesとしたとき (n_samples, n_stages, n_periods+1)。
network_base_stock_simulation
network_base_stock_simulation (G, n_samples, n_periods, demand, capacity, LT, ELT, b, h, S, phi, alpha)
ネットワーク型定期発注方策に対するシミュレーションと微分値の計算
初期基在庫レベルとエシェロンリード時間を計算する関数 initial_base_stock_level
定期発注方策を仮定したときの、エシェロンリード時間を計算し、それをもとに基在庫レベルを計算して返す関数。 エシェロンリード時間は、最終需要地点以外の点に対しては、1日を加えて計算する。
initial_base_stock_level
initial_base_stock_level (G, LT, mu, z, sigma)
初期基在庫レベルとエシェロンリード時間の計算
network_base_stock_simulation関数を利用した在庫最適化
上で作成した関数を用いて、最適化を行う。network_base_stock_simulationは、微分値を返すので、最急降下法を適用して最適値を探索する。 微分値の2乗和がepsilonを下回ったら終了する。
G = SCMGraph()
z = 1.65
b = np.array([0.,100.,100.])
h = np.array([1., 5., 2.])
mu = np.array([300., 200., 100.])
sigma = np.array([12., 10., 15.])
capacity = np.array([1320., 1120., 1230.])
G.add_edges_from([(0, 1), (0, 2)])
LT = np.array([3, 1, 2])
ELT = np.zeros(len(G))
phi = {(0, 1): 1, (0, 2): 1}
alpha = {(0, 1): 0.5, (0, 2): 0.5}
n_samples = 100
n_periods = 1000
demand ={} #需要量
for i in G:
if G.out_degree(i) == 0:
demand[i] = np.random.normal(mu[i], sigma[i], (n_samples, n_periods))
# エシェロンリード時間と初期基在庫レベルの設定
ELT, S = initial_base_stock_level(G, LT, mu, z, sigma)
print("ELT=", ELT)
print("S=", S)
print("t: Cost |dC| S ")
epsilon = 0.01
for iter_ in range(100):
dC, cost, I = network_base_stock_simulation(G, n_samples, n_periods, demand, capacity, LT, ELT, b, h, S, phi, alpha)
sum_ = 0.
#print("dC=",dC)
for j in G:
sum_ += dC[j]**2
S[j] = S[j] - 1.*dC[j]
print(f"{iter_}: {cost:.2f}, {sum_:.5f}", S)
if sum_ <= epsilon:
breakELT= [6. 1. 2.]
S= [1848.49989691 216.5 235.00178567]
t: Cost |dC| S
0: 3019.95, 17.08926 [1847.62530563 217.49740973 238.91707905]
1: 3006.19, 5.82522 [1846.8067274 217.51097292 241.18753291]
2: 3000.89, 2.75480 [1846.02908948 217.50571214 242.65383682]
3: 2998.09, 1.62961 [1845.29737183 217.49139168 243.69977714]
4: 2996.28, 1.06417 [1844.60260002 217.47909228 244.46221195]
5: 2995.01, 0.72428 [1843.94828582 217.46319584 245.00617509]
6: 2994.07, 0.54494 [1843.32732419 217.45502006 245.40527113]
7: 2993.30, 0.43767 [1842.730011 217.45163114 245.68966556]
8: 2992.67, 0.35866 [1842.1640293 217.45166499 245.88543662]
9: 2992.12, 0.31603 [1841.61648417 217.44484704 246.01264073]
10: 2991.63, 0.28328 [1841.09019154 217.44626505 246.09199254]
11: 2991.18, 0.25641 [1840.5857877 217.44053849 246.13615565]
12: 2990.78, 0.23289 [1840.1034789 217.43167377 246.15003918]
13: 2990.40, 0.21733 [1839.63730977 217.43089205 246.1457369 ]
14: 2990.04, 0.19542 [1839.19629673 217.42285795 246.11627852]
15: 2989.72, 0.18277 [1838.77053194 217.42063879 246.07771032]
16: 2989.41, 0.16754 [1838.36472953 217.41741412 246.02429507]
17: 2989.13, 0.15640 [1837.97370051 217.41310713 245.96531407]
18: 2988.86, 0.14614 [1837.59639766 217.4098182 245.90386064]
19: 2988.61, 0.13544 [1837.23391051 217.40119201 245.84089142]
20: 2988.37, 0.12520 [1836.8848687 217.40228999 245.78289211]
21: 2988.14, 0.11705 [1836.54740286 217.40023727 245.72661672]
22: 2987.93, 0.11064 [1836.21885629 217.39874373 245.67472198]
23: 2987.71, 0.10247 [1835.90308804 217.39500345 245.62232573]
24: 2987.52, 0.09693 [1835.59618264 217.40030404 245.57027426]
25: 2987.32, 0.09327 [1835.29460321 217.40133181 245.52210444]
26: 2987.13, 0.08379 [1835.00956215 217.39951229 245.47171922]
27: 2986.96, 0.08055 [1834.72877887 217.39764763 245.43037613]
28: 2986.79, 0.07318 [1834.46321624 217.39425339 245.37892772]
29: 2986.64, 0.06854 [1834.20645251 217.39259184 245.32788804]
30: 2986.49, 0.06316 [1833.95949445 217.3895499 245.28136566]
31: 2986.35, 0.05834 [1833.72243734 217.38608544 245.23517302]
32: 2986.21, 0.05304 [1833.49542662 217.38626567 245.19632617]
33: 2986.08, 0.04822 [1833.27944085 217.3870057 245.15668505]
34: 2985.96, 0.04516 [1833.0698292 217.38347793 245.12192358]
35: 2985.85, 0.04205 [1832.86827297 217.38137318 245.08422204]
36: 2985.74, 0.03913 [1832.67413149 217.38133212 245.04626724]
37: 2985.63, 0.03586 [1832.4898897 217.3808698 245.00250501]
38: 2985.54, 0.03389 [1832.31055889 217.37865597 244.96099329]
39: 2985.45, 0.03082 [1832.14016615 217.37908883 244.91872806]
40: 2985.36, 0.02814 [1831.97646732 217.3801999 244.88204575]
41: 2985.28, 0.02513 [1831.82350194 217.37479015 244.8407684 ]
42: 2985.21, 0.02265 [1831.67971848 217.37178324 244.79644754]
43: 2985.14, 0.02048 [1831.54170044 217.37143618 244.7586381 ]
44: 2985.08, 0.02011 [1831.40387548 217.377215 244.72575092]
45: 2985.01, 0.01788 [1831.27363076 217.37646674 244.6955142 ]
46: 2984.95, 0.01682 [1831.14750214 217.37581502 244.66525365]
47: 2984.89, 0.01627 [1831.02248436 217.37510563 244.64002069]
48: 2984.83, 0.01352 [1830.91097271 217.37036853 244.60741999]
49: 2984.78, 0.01248 [1830.80391694 217.37170715 244.57547878]
50: 2984.73, 0.01153 [1830.70035915 217.36954778 244.54720106]
51: 2984.69, 0.01034 [1830.60259375 217.37002131 244.51926937]
52: 2984.64, 0.00965 [1830.50919519 217.36718115 244.48901697]#可視化(最初のサンプルを表示)
# from plotly.subplots import make_subplots
# fig = make_subplots(rows=3, cols=1, subplot_titles= ["Stage " + str(i) for i in range(3)] )
# for j in range(3):
# trace = go.Scatter(
# x= list(range(n_periods)),
# y= I[0,j,:],
# mode = 'markers + lines',
# marker= dict(size= 5,
# line= dict(width=1),
# opacity= 0.3
# ),
# name ="Stage "+str(j)
# )
# fig.add_trace(
# trace,
# row=j+1, col=1
# )
# fig.update_layout(height=1000,title_text=f"Inventories for all stages", showlegend=False)
# plotly.offline.plot(fig);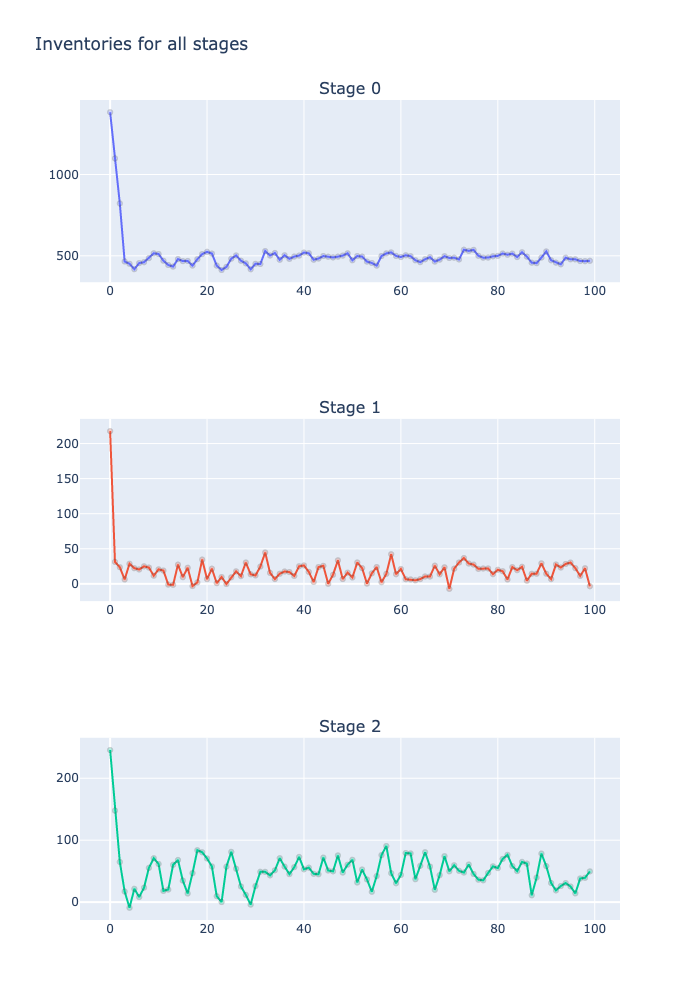
#hide ## 顧客の需要予測と安全在庫
上では、定常なランダム需要を仮定して、安全在庫量の最適化を行なったが、実際問題においては需要は定常とは限らない。
過去の需要系列demand_dfをもとに、Prophetによる予測を行う関数 forecastを準備する。 比較として、(需要の定常性を仮定して)平均と標準偏差も算出する。
引数:
- demand_df: 需要の系列を表すデータフレーム。顧客Cust、製品Prod,日時Date、需要量demandの列をもつものと仮定する。
- agg_period: 集約を行う期。例えば1週間を1期とするなら”1w”とする。既定値は1日(“1d”)
- forecast_period: 予測を行う未来の期数。既定値は1
返値:
以下の情報を列情報にもつデータフレーム
- mean: 需要の平均
- std : 需要の標準偏差
- 0..forecast_period-1: Prophetによる予測から計算された未来のforecast_periods 期分の最大在庫量
#hide ### forecast関数の使用例
1週間を1期として、30期を予測。
非常に時間がかかるので、注意。
#hide ## Prophetによる予測と需要の平均・標準偏差を用いた安全在庫量の比較と可視化
Prophetによる可視化
#hide ## 非定常な需要予測をもとにした基在庫レベルの最適化
以下では、実際問題を想定して、非定常な需要をもとに、安全在庫量を計算することを考える。
過去の需要系列demand_dfをもとに、Prophetによる予測サンプルを生成し、それに基づいたシミュレーションベースの基在庫レベルの 最適化を行う関数base_stock_prophetを準備する。
引数:
- demand_df: 需要の系列を表すデータフレーム。顧客Cust、製品Prod,日時Date、需要量demandの列をもつものと仮定する。
- agg_period: 集約を行う期。例えば1週間を1期とするなら”1w”とする。既定値は1日(“1d”)
- forecast_period: 予測を行う未来の期数。既定値は1
TODO: 今は、リード時間等は決め打ちだが、入力値とする。
返値:
以下の情報を列情報にもつデータフレーム
- mean: 需要の平均
- std : 需要の標準偏差
- S: 基在庫レベル
- cost: 1期間の平均費用
#hide ### base_stock_prophet関数の使用例
安全在庫配置モデル
動的最適化
#hide
ここでは,ネットワークが木状になっている場合について考え,動的最適化による厳密解法を示す.
木ネットワークモデルは,閉路を含まない有向グラフ \(G=(N,A)\) 上で義される. ここでは,\(G\) を無向グラフにしたものが木であると仮定する. 点集合 \(N\) は在庫地点を表し,枝 \((i,j) \in A\) が存在するとき,在庫地点 \(i\) は在庫地点 \(j\) に補充 を行うことを表す.複数の在庫地点から補充を受ける点においては,補充された各々の品目を用いて 別の品目を生産すると考える.
点 \(i\) における品目の生産時間は,\(T_i\) 日である. \(T_i\) には各段階における生産時間の他に,待ち時間および輸送時間も含めて考える.
このとき点 \(j\) は,複数の在庫地点から補充を受けるので,点 \(j\) が品目を発注してから,すべての品目が揃うまで生産を開始できない.
点上で生産される品目は,点によって唯一に定まるものと仮定する. このとき,点と品目を表す添え字は同一であると考えられるので, 有向グラフ \(G=(N,A)\) は部品展開表を意味することになる. \((i,j) \in A\) のとき,点 \(j\) 上の品目 \(j\) は,点 \(i\) から補充される品目 \(i\) をもとに生産される. 品目 \(j\) を生産するのに必要な品目 \(i\) の量を \(\phi_{ij}\) と記す.
需要は,後続する点をもたない点 \(j\) 上で発生するものとし, その \(1\) 日あたりの需要量は,期待値 \(\mu_j\) の定常な分布をもつものとする. 点 \(j\) における \(t\) 日間における需要の最大値を \(D_j(t)\) 記す.
直接の需要をもたない点(後続点をもつ点) \(i\) に対する需要量の期待値 \(\mu_i\) は, \[ \mu_i = \sum_{(i,j) \in A} \phi_{ij} \mu_j \] と計算できる.
点 \(i\) に対する\(t\) 日間における需要の最大値 \(D_i(t)\) は, \[ D_i(t)= t \mu_i +\left( \sum_{(i,j) \in A} \phi_{ij} (D_j(t)-t \mu_j)^p \right)^{1/p} \] と計算されるものと仮定する.
ここで,\(p (\geq 1)\) は定数である. \(p\) が大きいほど,需要の逆相関が強いことを表す. 点 \(j\) 上での需要が常に同期していると仮定した場合には \(p=1\) が, 点 \(j\) 上での需要が独立な正規分布にしたがうと仮定した場合には \(p=2\) が推奨される.
点 \(i\) の保証リード時間を \(L_i\) と記す. ここでは,各点 \(i\) に対して,保証リード時間の下限は \(0\) とし,上限は \(\bar{L}_i\) であるとする.
点 \(j\) が品目を発注してから,すべての品目が 揃うまでの時間(日数)を入庫リード時間とよび, \(LI_j\) と記す.
点 \(j\) における入庫リード時間 \(LI_j\) は,以下の式を満たす. \[ L_i \leq LI_j \ \ \ \forall (i,j) \in A \]
入庫リード時間 \(LI_i\) に生産時間 \(T_i\) を加えたものが,補充の指示を行ってから生産を完了するまでの時間となる. これを,補充リード時間とよぶ. 補充リード時間から、保証リード時間 \(L_i\) を減じた時間内の最大需要に相当する在庫を保持していれば,在庫切れの心配がないことになる. 補充リード時間から \(L_i\) を減じた時間(\(L_{i+1}+T_i-L_i\))を正味補充時間とよぶ.
点 \(i\) における安全在庫量 \(I_i\) は,正味補充時間内における最大需要量から平均需要量を減じた量であるので, \[ I_i= D(LI_{i}+T_i-L_i) - (LI_{i}+T_i-L_i) \mu_i \] となる.
記述を簡単にするために,点 \(i\) において,保証リード時間が \(L\), 入庫リード時間が \(LI\) のときの安全在庫費用を表す,以下の関数 \(HC_i(L,LI)\) を導入しておく.
\[ HC_i (L,LI)=h_i \left\{ D(LI+T_i-L) - (LI+T_i-L) \mu_i \right\} \]
上の記号を用いると,木ネットワークモデルにおける安全在庫配置問題は,以下のように定式化できる.
\[ \begin{array}{l l l } minimize & \sum_{i \in N} HC_i (L_i,LI_i) & \\ s.t. & L_i \leq LI_{i}+T_i & \forall i \in N \\ & L_i \leq LI_j & \forall (i,j) \in A \\ & 0 \leq L_i \leq \bar{L}_i & \forall i \in N \end{array} \]
ここで,最初の制約式は,正味補充時間が非負であることを表す.
木ネットワークモデルにおける安全在庫配置問題に対する動的最適化アルゴリズムは,以下のように構成できる.
与えられた有向グラフ \(G=(N,A)\) を無向グラフにしたものを \(\bar{G}=(N,E)\) と記す. 動的計画法は,グラフ \(\bar{G}\) の葉側から順次再帰方程式を計算していく.
以下では,点集合 \(N\) は上のアルゴリズムによって得られた順序で \(1,2,\cdots,|N|\) と番号がついているものと仮定する. 各点 \(k \in N\) に対して,点集合 \(\{1,2,\cdots,k\}\) の中で,点 \(k\) から \(\bar{G}\) 上で到達可能な点の集合 を \(N_k\) と記す. 点集合 \(N_k\) が下流(需要地点側)の点に対して保証リード時間 \(L\) で補充するときの 最小費用を \(f_k(L)\), 点集合 \(N_k\) が上流(供給地点側)の点から入庫リード時間 \(LI\) で補充を受けるときの 最小費用を \(g_k(LI)\) と書く.
ここで,\(f_k(L)\) は,保証リード時間 \(L\) に対して非増加関数になっているとは限らない. これを非増加関数にするために,保証リード時間 \(L\) 「以下」で補充するときの最小費用 \(f^-_k(L)\) を導入する. 関数 \(f^-_k(L)\) は,以下のように計算される.
\[ f^-_k(L)= \min_{T_k -L \leq x \leq L} f_k(x) \]
ここで,下限 \(T_k -L\) は,正味補充時間 \(x+T_k-L\) が非負であることから導かれたものである.
同様に,関数 \(g_k(LI)\) を,入庫リード時間 \(LI\) に対して非減少関数としたものを \(g^-_k(LI)\) とする. 関数 \(g^-_k(LI)\) は,以下のように計算される.
\[ g^-_k(LI)= \min_{LI \leq y \leq LI+T_k} g_k(y) \]
ここで,上限 \(LI+T_k\) は,正味補充時間 \(LI+T_k-y\) が非負であることから導かれたものである.
点 \(k\) における保証リード時間が \(L\),入庫リード時間が \(LI\) のときの 点集合 \(N_k\) 全体での最小費用を \(c_k(L,LI)\) と書く. このとき,\(c,f,g,f^-,g^-\) 間の再帰方程式は,以下のようになる.
\[ c_k(L,LI) = HC_k(L,LI) +\sum_{(i,k) \in A, i<k} f^-_i(LI) +\sum_{(k,j) \in A, j<k} g^-_j(L) \] \[ f_k(L) =\min_{LI} c_k(L,LI) \] \[ g_k(LI) =\min_{L} c_k(L,LI) \] \[ f^-_k(L)= \min_{T_k -L \leq x \leq L} f_k(x) \] \[ g^-_k(LI)= \min_{LI \leq y \leq LI+T_k} g_k(y) \]
上の動的最適化アルゴリズムの計算量は,補充リード時間の最大値を \(L_{\max}\) としたとき,\(O(|N| L_{\max}^2)\) となる.
このモデルの拡張として,枝 \((i,j)\) 上での輸送時間 \(\tau_{ij}\) を考慮することが考えられる. これは,上の再帰方程式を \[ c_k(L,LI) = HC_k (L,LI) +\sum_{(i,k) \in A, i<k} f^-_i(LI-\tau_{ik}) +\sum_{(k,j) \in A, j<k} g^-_j(L+\tau_{kj}) \] と変更するだけで良い.もしくは、ダミーの点を点間に挿入することによっても処理できる。
上のアルゴリズムは,入力サイズを \(|N|\) としたときには,\(L_{\max}=\sum_{i \in N} T_i\) であるので,擬多項式時間である.
最大需要の計算と安全在庫費用の計算
引数: - G: 有向グラフ - ProcTime: 処理時間 - LTLB: 保証リード時間の下限 - LTUB: 保証リード時間の上限 - z: 安全在庫係数 - mu: 需要の平均 - sigma: 需要の標準偏差 - h: 在庫費用
返値: - Lmax: 正味補充時間(在庫日数)の上限 - MaxDemand: t (=0..Lmax) 日間の最大需要量 - SafetyCost: t (=0..Lmax) 日間の安全在庫費用
max_demand_compute
max_demand_compute (G, ProcTime, LTLB, LTUB, z, mu, sigma, h)
computing the max demand for t days and the safety stock cost when the net reprenishment time is t (t=0,…,MaxNRT(i)) This function is used in the safety stock allocation problem. Current verstion assumes that the demand has a normal distribution. retuen Lmax (maximum net reprenishment time +1), MaxDemand, SafetyCost
最大需要計算関数 max_demand_compute の適用例
G = SCMGraph()
G.add_edges_from([(0, 1), (0, 2)])
z = 1.65
h = np.array([1., 5., 2.])
mu = np.array([300., 200., 100.])
sigma = np.array([12., 10., 15.])
ProcTime = np.array([5, 5 ,5], int)
LTLB = np.array([0,0,0], int)
LTUB = np.array([10,1,2], int)
Lmax, MaxDemand, SafetyCost = max_demand_compute(G, ProcTime, LTLB, LTUB, z, mu, sigma, h)
print("Lmax=",Lmax)
print("MaxDemand=",MaxDemand)
print("SafetyCost=",SafetyCost)Lmax= 11
MaxDemand= [[ 0. 319.8 628.00142853 934.29460599 1239.6
1544.27414595 1848.49989691 2152.38587596 2456.00285707 2759.4
3062.61309767]
[ 0. 216.5 423.33452378 628.57883832 833.
1036.89512163 1240.41658076 1443.65489663 1646.66904756 1849.5
2052.17758139]
[ 0. 124.75 235.00178567 342.86825749 449.5
555.34268244 660.62487113 765.48234495 870.00357134 974.25
1078.26637209]]
SafetyCost= [[ 0. 19.8 28.00142853 34.29460599 39.6
44.27414595 48.49989691 52.38587596 56.00285707 59.4
62.61309767]
[ 0. 82.5 116.6726189 142.89419162 165.
184.47560814 202.08290378 218.27448316 233.34523779 247.5
260.88790696]
[ 0. 49.5 70.00357134 85.73651497 99.
110.68536489 121.24974227 130.9646899 140.00714267 148.5
156.53274418]]安全在庫配置モデルに対する動的最適化アルゴリズム
引数: - G: 閉路を含まない有向グラフ(ただし無向グラフにしたものが木である必要がある。) - ProcTime: 処理時間(NumPyの配列) - LTLB: 保証リード時間の下限(NumPyの配列) - LTUB: 保証リード時間の上限(NumPyの配列) - z: 安全在庫係数 - mu: 需要の平均(NumPyの配列) - sigma: 需要の標準偏差(NumPyの配列) - h: 在庫費用(NumPyの配列)
返値: - total_cost: 最適費用 - Lstar: 最適保証リード時間 - NRT: 最適正味補充時間(在庫日数)
dynamic_programming_for_SSA
dynamic_programming_for_SSA (G, ProcTime, LTLB, LTUB, z, mu, sigma, h)
Solve the safety stock allocation problem by the dynamic programming algorithm. The network should be a tree. The algorithm is based on:
@incollection{Graves2003, author={S. C. Graves and S. Willems}, title={Supply Chain Design: Safety Stock Placement and Supply Chain Configuratation}, year={2003}, volume={11}, pages={95–132}, editor={A. G. {de} Kok and S.C. Graves}, publisher={Elsevier}, series={Handbook in Operations Research and Management Science}, chapter={3}, booktitle={Supply Chain Management: {D}esign, Coordination and Operation}, annote={ } }
dynamic_programming_for_SSA 関数の適用例
- 3点の例題
- 10点の直列多段階モデル
G =SCMGraph()
G.add_edges_from([(0, 1), (0, 2)])
z = 1.65
h = np.array([1., 5., 2.])
mu = np.array([300., 200., 100.])
sigma = np.array([12., 10., 15.])
ProcTime = np.array([5, 5 ,5], int)
LTLB = np.array([0,0,0], int)
LTUB = np.array([10,1,2], int)
total_cost, Lstar, NRT = dynamic_programming_for_SSA(G, ProcTime, LTLB, LTUB, z, mu, sigma, h)
print("TotalCost=",total_cost)
print("Lstar",Lstar)
print("NRT",NRT)TotalCost= 295.0106609291552
Lstar defaultdict(<function dynamic_programming_for_SSA.<locals>.<lambda>>, {0: 0, 1: 1, 2: 2})
NRT defaultdict(<function dynamic_programming_for_SSA.<locals>.<lambda>>, {0: 5, 1: 4, 2: 3})G = SCMGraph()
n = 10
edges =[(i,i-1) for i in range(n-1,0,-1)]
G.add_edges_from( edges )
z = 1.65
h = np.arange(n,0,-1)
mu = np.array([100.]*n)
sigma = np.array([10.]*n)
ProcTime = np.array([5]*n, int)
LTLB = np.zeros(n, int)
LTUB = np.array([0]+[0]*(n-1), int)
total_cost, Lstar, NRT = dynamic_programming_for_SSA(G, ProcTime, LTLB, LTUB, z, mu, sigma, h)
print("TotalCost=",total_cost)
print("Lstar",Lstar)
print("NRT",NRT)TotalCost= 2029.231689581059
Lstar defaultdict(<function dynamic_programming_for_SSA.<locals>.<lambda>>, {9: 0, 8: 0, 7: 0, 6: 0, 5: 0, 4: 0, 3: 0, 2: 0, 1: 0, 0: 0})
NRT defaultdict(<function dynamic_programming_for_SSA.<locals>.<lambda>>, {9: 5, 8: 5, 7: 5, 6: 5, 5: 5, 4: 5, 3: 5, 2: 5, 1: 5, 0: 5})安全在庫配置モデルに対するメタ解法
#hide
より実践的な方法として、一般ネットワークに対応したメタ解法が考えられる。以下では、
@book{book,
author = {Minner, Stefan},
year = {2000},
month = {01},
pages = {},
title = {Strategic Safety Stocks in Supply Chains},
volume = {490},
doi = {10.1007/978-3-642-58296-7},
series = {Lecture Notes in Economics and Mathematical Systems},
publisher ={Springer}
}に基づいたタブー探索によるメタ解法を示す。NumPyで近傍を高速に計算している点が特徴である。
準備として、安全在庫配置問題の定式化を,正味補充時間を \(NTR_i\) (net replenishment time)を変数とした定式化に変換することを考える。
\[ L_i = \max_{k: (k,i) \in A} \{ L_k \} + T_i - NRT_i \] を元の(保証リード時間と入庫リード時間を変数とした)定式化に代入する。
全ての供給地点(入次数が \(0\) の点)から点 \(i\) に至るパスの集合を \(PathTo_i\)、全ての供給地点から需要地点(出次数が \(0\) の点)に至る パスの集合を \(PATH\) とする。パス \(p\) に含まれる点の集合を \(N_p\) とすると、以下の定式化を得る。
\[ \begin{array}{l l l } minimize & \sum_{i \in N} \sum h_i \sigma_i \sqrt{NRT_i} & \\ s.t. & \max_{p \in PathTo_i} \sum_{i \in N_p} (T_i - NRT_i ) \geq 0 & \forall i \in N \\ & \sum_{i \in N_p} (NRT_i - T_i ) \geq 0 & \forall p \in PATH \\ & NRT_i \geq 0 & \forall i \in N \end{array} \]
点 \(i\) への最大入庫リード時間は、 \[ \max_{p \in PathTo_i} \sum_{i \in N_p \setminus \{ i \}} (T_i - NRT_i ) \] であるので、それに生産時間 \(T_i\) を加えたものが、最大補充リード時間 \(MaxLI_i\) になる。
また、点 \(i\) から需要地点に至るパスの集合を \(PathFrom_i\) と記すと、点 \(i\) の最小保証リード時間 \(MinLT_i\) は、 \[ \min_{p \in PathFrom_i} \sum_{i \in N_p \setminus \{ i \}} (NRT_i - T_i ) \] と書くことができる。
点 \(i\) の正味補充時間 \(NTR_i\) は、補充リード時間から保証リード時間を減じたもの(と\(0\)の大きい方)であるので、 上流の地点からの最大補充リード時間 \(MaxLI_i\) と下流の地点への最小保証リード時間 \(MinLT_i\) を用いて、 以下のように計算できる。
\[ NRT_i = \left[ MaxLI_i - MinLT_i \right]^+ \]
点ごとに、正の在庫を配置するか否かを表すベクトル \(b\) を与えたとき、最大補充リード時間 \(MaxLI_i\) は下流の地点から順に以下のように計算できる。
\[ MaxLI_i = \left\{ \begin{array}{ l l} T_i & \forall i \in 供給地点 \\ T_i + \max_{ (k,i) \in A } (1-b_k) MaxLI_k & それ以外 \end{array} \right. \]
これは、上流の地点が在庫地点の場合には、入庫リード時間が \(0\) になり、在庫地点でない場合には、正味補充時間が \(0\) になることを利用している。
また、最小保証リード時間 \(MinLT_i\) は上流の地点から順に以下のように計算できる。
\[ MinLT_i = \left\{ \begin{array}{ l l} LTUB_i & \forall i \in 需要地点 \\ \min_{ (i,j) \in A } NRT_j + MinLT_j - T_j & それ以外 \end{array} \right. \] ここで, \(LTUB_i\) は地点 \(i\) に対する保証リード時間の上限である.
同時に、正味補充時間 \(NRT_i\) も以下のように計算する。
\[ NRT_i = \left[ MaxLI_i - MinLT_i \right]^+ \]
全ての地点の正味補充時間が計算されたら、総費用は、安全在庫係数 \(z\)、需要の標準偏差 \(\sigma_i\)、在庫費用 \(h_i\) を用いて、以下のように評価できる。
\[ \sum h_i z \sigma_i \sqrt{ NRT_i } \]
近傍や探索方法については、種々のメタ解法が考えられるが、以下ではNumPyを用いて一度に評価値を計算するタブー探索を構築する。 また、複数製品に対して同時に評価値を計算することも可能である。
決定変数 \(b\) は、需要地点に対しては除外することができる。 \(b\) が使われるのは、 \(MaxLI\) の計算の部分だけであり、 需要地点には後続する点がないため、需要地点に対する \(b\) は解の評価に影響を与えないためである。
上の方法では、供給地点、需要地点のリード時間は \(0\) と仮定しているが、ダミーの点を追加したり、生産時間を変更することによって、保証リード時間の上下限付きの問題も解ける。
用語と記号:
- 保証リード時間 (guaranteer lead time, service time): \(L\)
- 生産時間 (production time): \(T\)
- 入庫リード時間 (incoming lead time): \(LI\)
- 補充リード時間 (replenishment lead time)
- 正味補充時間 (net replenishment time): \(NRT\)
- 最大補充リード時間: \(MaxLI\)
- 最小保証リード時間: \(MinLT\)
安全在庫配置モデルに対するタブー探索アルゴリズム tabu_search_for_SSA
引数: - G: 閉路を含まない有向グラフ - ProcTime: 処理時間(NumPyの配列);以下の配列はグラフGの点を列挙したときの順序(グラフに点を追加した順序)の順に保管してあるものとする. - LTUB: 保証リード時間上限(NumPyの配列) - z: 安全在庫係数 - mu: 需要の平均(NumPyの配列) - sigma: 需要の標準偏差(NumPyの配列) - h: 在庫費用(NumPyの配列) - max_iter: 最大反復数 - TLLB : タブー長の下限の初期値 - TLUB : タブー長の上限の初期値 - seed : 乱数の種
返値: - best_cost:最良値 - best_sol: 最良解(在庫を保持するなら1、否なら0の配列) - best_NRT: 最良解における正味補充時間(在庫日数) - best_MaxLI: 最良解における最大補充リード時間 - best_MinLT: 最良解における最小保証リード時間
tabu_search_for_SSA
tabu_search_for_SSA (G, ProcTime, LTUB, z, mu, sigma, h, max_iter=100, TLLB=1, TLUB=10, seed=1)
一般のネットワークの安全在庫配置モデルに対するタブー探索(mu未使用;NRT日の最大在庫量をシミュレーションもしくは畳み込みによって事前計算?もしくは正規分布で近似)
tabu_search_for_SSA関数の使用例
- 3点の例題
- 10点の直列多段階モデル
- ベンチマーク問題例
#3点の例題
G = SCMGraph()
G.add_edges_from([(0, 1), (0, 2)])
z = 1.65
h = np.array([1., 1., 1.])
mu = np.array([300., 200., 100.])
sigma = np.array([12., 10., 15.])
LTUB = np.zeros(3)
ProcTime = np.array([5, 4 ,3], int) # 動的最適化の例題と合わせるため、生産時間から保証リード時間上限を減じてある
best_cost, best_sol, best_NRT, best_MaxLI, best_MinLT = tabu_search_for_SSA(G, ProcTime, LTUB, z, mu, sigma, h, max_iter = 10, TLLB =1, TLUB =3, seed = 1)
print("最良値", best_cost)
print("最良解", best_sol)
print("正味補充時間", best_NRT)
print("最大補充リード時間", best_MaxLI)
print("最小保証リード時間", best_MinLT)最良値 119.50357133746822
最良解 [0 1 1]
正味補充時間 [0. 9. 8.]
最大補充リード時間 [5. 9. 8.]
最小保証リード時間 [5. 0. 0.]#4点の直列多段階の例題
# G = SCMGraph()
# n = 4
# # 点の順序を0,1,2... とするため
# for i in range(n):
# G.add_node(i)
# edges =[(i,i-1) for i in range(n-1,0,-1)]
# G.add_edges_from( edges )
# z = np.ones(n)
# h = np.array([40,30,20,10])
# mu = np.array([100.]*n)
# sigma = np.array([10.]*n)
# ProcTime = np.array([1,1,2,3], int)
# LTUB = np.array([0,0,0,0],int)
# best_cost, best_sol, best_NRT, best_MaxLI, best_MinLT = tabu_search_for_SSA(G, ProcTime, LTUB, z, mu, sigma, h, max_iter = 10, TLLB =1, TLUB =3, seed = 2)
# print("最良値", best_cost)
# print("最良解", best_sol)
# print("正味補充時間", best_NRT)
# print("最大補充リード時間", best_MaxLI)
# print("最小保証リード時間", best_MinLT)
# pos ={i:(n-i,0) for i in range(n) }
# stage_df, bom_df = make_df_for_SSA(G, pos, ProcTime, LTUB, z, mu, sigma, h, best_NRT, best_MaxLI, best_MinLT)
# stage_df.to_csv(folder_bom + "stage_ex0.csv")
# bom_df.to_csv(folder_bom + "bom_e01.csv")
# fig, G, pos = draw_graph_for_SSA_from_df(stage_df, bom_df)
# #fig.show()
# nx.draw(G, pos=pos)最良値 973.2050807568877
最良解 [1 0 0 1]
正味補充時間 [4. 0. 0. 3.]
最大補充リード時間 [4. 3. 2. 3.]
最小保証リード時間 [0. 3. 2. 0.]
#cost, stage_df, I, cost_list, phi_list = periodic_inv_opt_fit_one_cycle(stage_df, bom_df, max_iter = 100, n_samples = 10,
# n_periods = 100, seed = 1, lr_find=False, max_lr =0.1, moms=(0.85,0.95))#fig = plot_simulation(stage_df, I, n_periods =100, samples=5)
#plotly.offline.plot(fig);#10点の直列多段階モデル
G = SCMGraph()
n =8
# 点の順序を0,1,2... とするため
for i in range(n):
G.add_node(i)
edges =[(i,i-1) for i in range(n-1,0,-1)]
G.add_edges_from( edges )
z = 1.65
#h = np.arange(n,0,-1)
h = np.array([20,20,10,10,10,5,5,1])
mu = np.array([100.]*n)
sigma = np.array([10.]*n)
ProcTime = np.array([5]*n, int)
LTUB = np.zeros(n)
best_cost, best_sol, best_NRT, best_MaxLI, best_MinLT = tabu_search_for_SSA(G, ProcTime, LTUB, z, mu, sigma, h, max_iter = 10, TLLB =1, TLUB =3, seed = 1)
print("最良値", best_cost)
print("最良解", best_sol)
print("正味補充時間", best_NRT)
print("最大補充リード時間", best_MaxLI)
print("最小保証リード時間", best_MinLT)最良値 1905.4467494843116
最良解 [1 0 1 0 0 0 0 1]
正味補充時間 [10. 0. 25. 0. 0. 0. 0. 5.]
最大補充リード時間 [10. 5. 25. 20. 15. 10. 5. 5.]
最小保証リード時間 [ 0. 5. 0. 20. 15. 10. 5. 0.]#7点の一般型ネットワークの例題
n=7
G = SCMGraph()
for i in range(n):
G.add_node(i)
G.add_edges_from([(0, 2), (1, 2), (2,4), (3,4), (4,5), (4,6)])
z = np.full(len(G),1.65)
h = np.array([1,1,3,1,5,6,6])
mu = np.array([200,200,200,200,200,100,100])
sigma = np.array([14.1,14.1,14.1,14.1,14.1,10,10])
LTUB = np.array([0,0,0,0,0,3,1], int)
ProcTime = np.array([6,2,3,3,3,3,3], int) # 動的最適化の例題と合わせるため、生産時間から保証リード時間上限を減じてある
best_cost, best_sol, best_NRT, best_MaxLI, best_MinLT = tabu_search_for_SSA(G, ProcTime, LTUB, z, mu, sigma, h, max_iter = 10, TLLB =1, TLUB =3, seed = 1)
print("最良値", best_cost)
print("最良解", best_sol)
print("正味補充時間", best_NRT)
print("最大補充リード時間", best_MaxLI)
print("最小保証リード時間", best_MinLT)
# pos = G.layout()
# stage_df, bom_df = make_df_for_SSA(G, pos, ProcTime, LTUB, z, mu, sigma, h, best_NRT, best_MaxLI, best_MinLT)
# stage_df.to_csv(folder_bom + "stage_ex1.csv")
# bom_df.to_csv(folder_bom + "bom_ex1.csv")
# fig, G, pos = draw_graph_for_SSA_from_df(stage_df, bom_df)
# #fig.show()
# nx.draw(G, pos=pos)最良値 514.8330943986502
最良解 [1 1 0 0 1 0 1]
正味補充時間 [6. 2. 0. 0. 6. 0. 2.]
最大補充リード時間 [6. 2. 3. 3. 6. 3. 3.]
最小保証リード時間 [0. 0. 3. 3. 0. 3. 1.]# stage_df = pd.read_csv(folder_bom + "stage_ex1.csv")
# bom_df = pd.read_csv(folder_bom + "bom_ex1.csv")
# best_cost, stage_df, bom_df, fig = solve_SSA(stage_df, bom_df)
# stage_df| Unnamed: 0 | name | net_replenishment_time | max_guaranteed_LT | processing_time | replenishment_LT | guaranteed_LT | z | average_demand | sigma | h | b | capacity | x | y | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 6.0 | 0 | 6 | 6.0 | 0.0 | 1.65 | 200 | 14.1 | 1 | 8.8 | 2000.0 | 0 | 0 |
| 1 | 1 | 1 | 2.0 | 0 | 2 | 2.0 | 0.0 | 1.65 | 200 | 14.1 | 1 | 8.8 | 2000.0 | 0 | 2 |
| 2 | 2 | 2 | 0.0 | 0 | 3 | 3.0 | 3.0 | 1.65 | 200 | 14.1 | 3 | 26.3 | 2000.0 | 1 | 0 |
| 3 | 3 | 3 | 0.0 | 0 | 3 | 3.0 | 3.0 | 1.65 | 200 | 14.1 | 1 | 8.8 | 2000.0 | 0 | 1 |
| 4 | 4 | 4 | 6.0 | 0 | 3 | 6.0 | 0.0 | 1.65 | 200 | 14.1 | 5 | 43.9 | 2000.0 | 2 | 0 |
| 5 | 5 | 5 | 0.0 | 3 | 3 | 3.0 | 3.0 | 1.65 | 100 | 10.0 | 6 | 52.7 | 1000.0 | 3 | 0 |
| 6 | 6 | 6 | 2.0 | 1 | 3 | 3.0 | 1.0 | 1.65 | 100 | 10.0 | 6 | 52.7 | 1000.0 | 3 | 1 |
# cost, stage_df, I, cost_list, phi_list = periodic_inv_opt_fit_one_cycle(stage_df, bom_df, max_iter = 1000, n_samples = 10,
# n_periods = 100, seed = 1, lr_find=False, max_lr =6.0, moms=(0.85,0.95))ELT= [21. 17. 13. 13. 11. 1. 3.]
S= [4306.61362354 3495.92405238 2683.88315042 2683.88315042 2277.16127575
116.5 328.57883832]
t: Cost |dC| S
0: 16082.26, 2384121.79078 [4306.61362354 3495.92405238 2683.88315042 2683.88315042 2277.16127575
116.5 328.57883832]
50: 16064.14, 55008642.72020 [4304.02992277 3498.69251131 2679.18513171 2686.70283345 2274.05919829
119.66406743 344.12554439]
100: 16065.15, 5026167.93997 [4305.81174737 3498.76846583 2678.40095109 2686.61752507 2273.55957572
120.84683667 340.51778989]
150: 16061.73, 109999436.60082 [4303.16094465 3502.71988907 2672.66577621 2685.7481414 2279.55090957
120.56158991 341.11925034]
200: 16065.26, 5222011.53967 [4312.76590192 3492.32576853 2681.96668542 2684.31474986 2272.03751252
120.58780939 340.94018907]
250: 16062.70, 28978730.42492 [4312.2184163 3492.26969664 2681.9034483 2682.24835951 2272.76515243
120.68572406 341.01899329]
300: 16083.57, 11181822.94933 [4311.15839432 3493.40225594 2680.87064495 2703.05431135 2273.45772924
120.83500766 341.05489796]
350: 16079.60, 5321.32095 [4307.69066274 3497.77039769 2676.08815218 2700.18398616 2277.70718962
120.48910017 340.87407204]
400: 16075.63, 63551.03463 [4307.64834193 3497.78911077 2676.32680439 2696.23356042 2277.16193522
120.79860651 341.06201143]
450: 16071.07, 11328.58722 [4308.05463524 3497.72018746 2676.22034128 2691.43264714 2276.99734823
120.79266494 340.98458816]
500: 16065.01, 29646.92335 [4307.82339303 3497.72585609 2676.17683586 2685.7119275 2277.17212027
120.96624478 341.06602026]
550: 16058.02, 105022.66152 [4307.27597593 3497.85808953 2676.04251307 2679.3697765 2277.57701891
120.59324681 341.0362919 ]
600: 16126.80, 78916.21887 [4307.84910082 3497.47376626 2676.02237295 2747.63728074 2276.2455183
120.83557065 340.82623601]
650: 16128.17, 75923.78927 [4307.12100365 3497.49710856 2675.84794371 2749.80816501 2277.04754176
120.91189266 340.91285357]
700: 16126.23, 105024.49925 [4306.96412636 3497.52463691 2675.65866046 2748.08164634 2277.39564944
119.95046856 341.00884094]
750: 16125.26, 25019.64204 [4307.6174081 3497.33181103 2675.81217298 2746.63589639 2276.7266567
120.89359202 340.92325567]
800: 16123.20, 107188.28867 [4306.65730431 3497.56396823 2675.5592795 2745.52972634 2277.63620685
120.55485679 340.81960078]
850: 16122.84, 105773.51829 [4307.15776745 3497.487481 2675.42919782 2744.77972635 2277.49292265
120.53375714 341.01864899]
900: 16122.64, 7777.36243 [4307.44336725 3497.45996464 2675.33777062 2744.35799326 2277.41409729
120.54642398 340.86674134]
950: 16122.86, 14175.35550 [4307.9300071 3497.38395884 2675.23658045 2744.191592 2277.26791974
120.55581911 340.85063693]
Best: 16023.43, 0.00965 [4307.50553981 3497.77958792 2676.18044936 2656.18886109 2277.33810851
121.21002819 341.04645203]# fig = plot_simulation(stage_df, I, n_periods =100, samples=5)
# plotly.offline.plot(fig);# fig = plot_inv_opt_lr_find(cost_list, phi_list)
# plotly.offline.plot(fig);Willemsのベンチマーク問題例の読み込み
Willemsのデータ(XMLファイル)を読み込みグラフのデータを組み立てる。
引数: - file_name: Willemsのデータ番号;“01” から “38” までの「文字列」を入れる。
返値: - G: SCMGraphのインスタンス;閉路を含まない有向グラフ - pos: 点の座標;点の名前をキー、(x,y)座標を値としてもつ辞書
グラフは、点の属性として以下の値を保管してある。
- stageName: 点の名称
- stageCost: 点で付加される費用(浮動小数点数の文字列)
- relDepth: 点の深さ(下流(需要側)から0,1,2,…)
- stageClassification: 点の種類
- avgDemand: 平均需要量(整数の文字列)
- stDevDemand: 需要の標準偏差(整数の文字列)
- maxServiceTime: 最大サービス時間(保証リード時間)(整数の文字列)
- serviceLevel: サービス率(浮動小数点数の文字列)
- stageTime: 生産時間(整数の文字列)
- xPos: \(x\) 座標(整数の文字列)
- yPos: \(y\) 座標(整数の文字列)
read_willems
read_willems (file_name)
Willemsのベンチマーク問題例の読み込み関数
read_wellems関数の使用例
G, pos = read_willems(file_name= folder+"bom/03.xml")
nx.draw(G, pos=pos, with_labels=True, node_color="Yellow")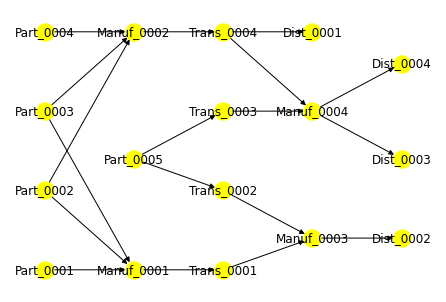
#Pyvisの利用
net = pyvis.network.Network(height='500px', width='500px', directed = True,
notebook = True, bgcolor='#ffffff', font_color=False, layout=1, heading='')
net.from_nx(G)
#net.show("example.html")点の属性は、以下のように点に付随する属性の辞書、もしくはget_node_attributesメソッドを用いてアクセスできる。
for i in G: print( G.nodes[i]["stageTime"], end=" " )
print( nx.get_node_attributes(G, "maxServiceTime") )10 10 28 15 10 0 0 0 {'Retail_0001': '0', 'Retail_0002': '0', 'Retail_0003': '0'}在庫費用、需要量、需要の標準偏差の計算
ベンチマークデータからタブー探索で必要なデータを抽出し、必要なデータを準備する。 各地点には付加された費用と生産時間、需要地点には需要と標準偏差と保証リー時間上限(サービス時間)が入っている。 すべての点に対して、在庫費用と需要・標準偏差など、安全在庫配置モデルの計算に必要なデータを計算する関数を準備しておく。
引数:
- G: ベンチマーク問題例のグラフ
返値:
- ProcTime: 処理時間 (NumPy配列)
- LTUB: 保証リード時間上限 (NumPy配列)
- z: 安全在庫係数 (NumPy配列)
- mu: 需要の平均 (NumPy配列)
- sigma: 需要の標準偏差 (NumPy配列)
- h: 在庫費用 (NumPy配列)
extract_data_for_SSA
extract_data_for_SSA (G)
ベンチマークデータからタブー探索で必要なデータを抽出する関数
extract_data_for_SSA関数とタブー探索の実行例
mu, sigma, h, z, ProcTime, LTUB = extract_data_for_SSA(G)
best_cost, best_sol, best_NRT, best_MaxLI, best_MinLT = \
tabu_search_for_SSA(G, ProcTime, LTUB, z, mu, sigma, h, max_iter = len(G)*2,
TLLB =int(np.sqrt(len(G))/2), TLUB =int(np.sqrt(len(G))), seed = 1)
print("最良値", best_cost)
print("最良解", best_sol)
print("正味補充時間", best_NRT)
print("最大補充リード時間", best_MaxLI)
print("最小保証リード時間", best_MinLT)cost= 17431180.517088737 [1 1 1 1 1 1 1 1 1 0 0 1 0 1 1 0 0]
最良値 14635043.250984032
最良解 [1 1 1 1 0 1 0 0 0 0 1 0 1 1 0 0 0]
正味補充時間 [ 3. 13.2 16.3 16.2 0. 47.5 0. 0. 0. 0. 16. 0. 31. 57.
0. 0. 0. ]
最大補充リード時間 [ 3. 13.2 16.3 16.2 57. 47.5 12. 12. 45. 37.5 53.5 26. 31. 59.
2. 2. 2. ]
最小保証リード時間 [ 0. 0. 0. 0. 57. 0. 12. 12. 45. 37.5 37.5 37.5 0. 2.
2. 2. 2. ]#在庫の有無を色で区別し、正味補充時間(在庫量)をノードの大きさで表して描画
nx.draw(G, pos=pos, with_labels=True, node_size=best_NRT*50,node_color=best_sol)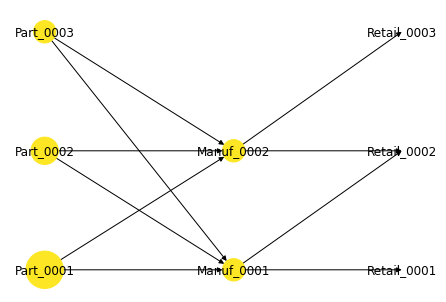
print("best obj.=", best_cost)
print("best sol.=", best_sol)
print("best NRT=", best_NRT)best obj.= 14635043.250984032
best sol.= [1 1 1 1 0 1 0 0 0 0 1 0 1 1 0 0 0]
best NRT= [ 3. 13.2 16.3 16.2 0. 47.5 0. 0. 0. 0. 16. 0. 31. 57.
0. 0. 0. ]安全在庫配置問題の結果を描画する関数 draw_graph_for_SSA
点の大きさが在庫量(正味補充時間)を表し、点の色(色の濃いものほど小さい)が保証リード時間を表す。
引数:
- G: 閉路を含まない有向グラフ
- pos: 点の座標を保管した辞書
- best_NRT: 最良解における正味補充時間(在庫日数)
- best_MaxLI: 最良解における最大補充リード時間
- best_MinLT: 最良解における最小保証リード時間
返値: - Plotlyの図オブジェクト
draw_graph_for_SSA
draw_graph_for_SSA (G, pos, best_NRT, best_MaxLI, best_MinLT)
安全在庫配置問題の結果をPlotlyで描画する関数
draw_graph_for_SSAの使用例
fig = draw_graph_for_SSA(G, pos, best_NRT, best_MaxLI, best_MinLT)
#plotly.offline.plot(fig); #htmlを吐きたいときには、ここを生かす。
#fig.show()安全在庫配置問題の結果をデータフレームに変換する関数 make_df_for_SSA
点(stage)の情報を保管したデータフレームと枝(部品展開表;bom)の情報を保管したデータフレームを構築する。
引数: - G: 閉路を含まない有向グラフ - pos: 点の座標を保管した辞書 - ProcTime: 処理時間 (NumPy配列) - LTUB: 保証リード時間上限 (NumPy配列) - z: 安全在庫係数 (NumPy配列) - mu: 需要の平均 (NumPy配列) - sigma: 需要の標準偏差 (NumPy配列) - h: 在庫費用 (NumPy配列) - best_NRT: 最良解における正味補充時間(在庫日数) - best_MaxLI: 最良解における最大補充リード時間 - best_MinLT: 最良解における最小保証リード時間
返値: - 点(stage)の情報を保管したデータフレーム
name: 点名
net_replenishment_time: 正味補充時間
max_guaranteed_LT: 保証リード時間上限
processing_time: 処理時間
replenishment_LT: 補充リード時間
guaranteed_LT: 保証リード時間
z: 安全在庫係数
average_demand: 需要の平均
sigma: 需要の標準偏差
h: 在庫費用
b: 品切れ費用(在庫費用hとサービス率pをもとにp=b/(b+h)になるように計算)
capacity: 生産容量(需要量の平均の10倍と設定しておく.)
x: 点のx座標
y: 点のy座標
枝(部品展開表;bom)の情報を保管したデータフレーム
child: 子製品名
parent: 親製品名
units: 親製品を製造するのに必要な子製品の数(すべて1に設定)
allocation: 在庫を複数の下流の点に配分するときの割合(在庫シミュレーション最適化で用いる.)
make_df_for_SSA
make_df_for_SSA (G, pos, ProcTime, LTUB, z, mu, sigma, h, best_NRT, best_MaxLI, best_MinLT)
点(stage)と枝(bom)を保管したデータフレームを返す関数
make_df_for_SSAの使用例
# stage_df, bom_df = make_df_for_SSA(G, pos, ProcTime, LTUB, z, mu, sigma, h, best_NRT, best_MaxLI, best_MinLT)
# #stage_df.to_csv(folder_bom + "ssa02.csv")
# stage_df| name | net_replenishment_time | max_guaranteed_LT | processing_time | replenishment_LT | guaranteed_LT | z | average_demand | sigma | h | b | capacity | x | y | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Manuf_0001 | 10.0 | 0.0 | 10.0 | 10.0 | 0.0 | 1.644854 | 298.0 | 36.633651 | 65.0 | 565.2 | 2980.0 | 176 | 32 |
| 1 | Manuf_0002 | 10.0 | 0.0 | 10.0 | 10.0 | 0.0 | 1.644854 | 120.0 | 2.236068 | 62.0 | 539.2 | 1200.0 | 176 | 96 |
| 2 | Part_0001 | 28.0 | 0.0 | 28.0 | 28.0 | 0.0 | 1.644854 | 418.0 | 36.701831 | 12.0 | 104.4 | 4180.0 | 32 | 32 |
| 3 | Part_0002 | 15.0 | 0.0 | 15.0 | 15.0 | 0.0 | 1.644854 | 418.0 | 36.701831 | 5.0 | 43.5 | 4180.0 | 32 | 96 |
| 4 | Part_0003 | 10.0 | 0.0 | 10.0 | 10.0 | 0.0 | 1.644854 | 418.0 | 36.701831 | 9.0 | 78.3 | 4180.0 | 32 | 160 |
| 5 | Retail_0001 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.644854 | 253.0 | 36.620000 | 65.0 | 565.2 | 2530.0 | 304 | 32 |
| 6 | Retail_0002 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.644854 | 45.0 | 1.000000 | 127.0 | 1104.4 | 450.0 | 304 | 96 |
| 7 | Retail_0003 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.644854 | 75.0 | 2.000000 | 62.0 | 539.2 | 750.0 | 304 | 160 |
#bom_df.to_csv(folder_bom + "ssa_bom02.csv")
#bom_df.head()| child | parent | units | allocation | |
|---|---|---|---|---|
| 0 | Manuf_0001 | Retail_0001 | 1 | 0.5 |
| 1 | Manuf_0001 | Retail_0002 | 1 | 0.5 |
| 2 | Manuf_0002 | Retail_0002 | 1 | 0.5 |
| 3 | Manuf_0002 | Retail_0003 | 1 | 0.5 |
| 4 | Part_0001 | Manuf_0001 | 1 | 0.5 |
データフレームからデータの図を描画する関数 draw_graph_for_SSA_from_df
引数: - 点(stage)の情報を保管したデータフレーム - 枝(部品展開表;bom)の情報を保管したデータフレーム
返値: - fig : Plotlyの図オブジェクト - G : グラフ - pos : 点の座標を表す辞書
draw_graph_for_SSA_from_df
draw_graph_for_SSA_from_df (stage_df, bom_df)
データフレームを入れると、安全在庫配置問題のデータをPlotlyで描画する関数
draw_graph_for_SSA_from_df関数の使用例
# fig, G, pos = draw_graph_for_SSA_from_df(stage_df, bom_df)
# #plotly.offline.plot(fig)
# nx.draw(G, pos=pos)
全てのベンチマークデータをcsvファイルに変換
# for i in range(1, 39):
# fn = str(i)
# if len(fn) == 1:
# fn = "0"+fn
# #print(i)
# G, pos = read_willems(file_name=fn)
# mu, sigma, h, z, ProcTime, LTUB = extract_data_for_SSA(G)
# n = len(G)
# best_NRT = np.zeros(n)
# best_MaxLI = np.zeros(n)
# best_MinLT =np.zeros(n)
# stage_df, bom_df = make_df_for_SSA(
# G, pos, ProcTime, LTUB, z, mu, sigma, h, best_NRT, best_MaxLI, best_MinLT)
# stage_df.to_csv("../data/bom/ssa"+fn+".csv")
# bom_df.to_csv("../data/bom/ssa_bom"+fn+".csv")データフレームを入力すると、一般のネットワークの安全在庫配置モデルに対するタブー探索を行う関数 solve_SSA
引数:
- stsge_df : 点の情報を保管したデータフレーム
- bom_df : 枝の情報を保管したデータフレーム
返値:
- stage_df : (最適化された後の)点の情報を保管したデータフレーム
- bom_df : (最適化された後の)枝の情報を保管したデータフレーム
- fig : Plotlyの図オブジェクト
solve_SSA
solve_SSA (stage_df, bom_df)
データフレームを入力とした一般のネットワークの安全在庫配置モデルに対するタブー探索
solve_SSA関数の使用例
# stage_df = pd.read_csv(folder_bom + "ssa03.csv")
# bom_df = pd.read_csv(folder_bom + "ssa_bom03.csv")
# best_cost, stage_df, bom_df, fig = solve_SSA(stage_df, bom_df)
# stage_df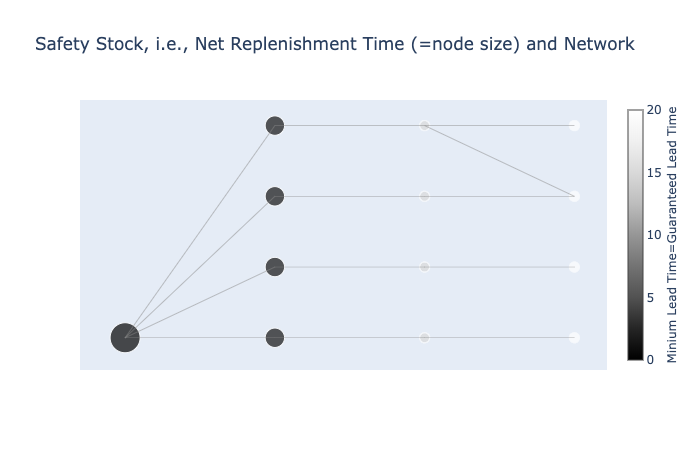
データフレームをもとに定期発注方策最適化を行う関数 periodic_inv_opt
定期発注方策の仮定の下では,保証リード時間は \(0\) とみなす必要位がある. また,各点のリード時間は,安全在庫配置モデルの補充リード時間 (replenishment leadtime: best_MaxLI) に (定期発注方策なので) \(1\) を加えたもの相当する.
ただし出荷を待っている(すでに下流からの注文がある;保証リード時間に相当する)在庫も含めた在庫レベルを考えるものとする.
保証リード時間中の需要は確定値なので考慮する必要はない. 保証リード時間 \(+1\) 日をリード時間と考える.
最適な \((s,S)\) を近似的に求め,シミュレーションを行う.
安全在庫配置の結果がすでに入ったデータフレームをもとに,定期発注方策の最適化を行う.
需要が負になることが頻繁に発生する場合には,基在庫レベルを多少大きくする必要があり,どの程度大きくすれば良いかは実験を行う必要がある.
periodic_inv_opt
periodic_inv_opt (stage_df, bom_df, max_iter=1, n_samples=10, n_periods=100, seed=1)
データフレームを入力とした定期発注方策最適化
periodic_inv_opt関数の使用例
# stage_df = pd.read_csv(folder_bom + "ssa02.csv", index_col=0)
# bom_df = pd.read_csv(folder_bom + "ssa_bom02.csv", index_col=0)
# best_cost, stage_df, bom_df, fig = solve_SSA(stage_df, bom_df)
# cost, stage_df, I = periodic_inv_opt(stage_df, bom_df, max_iter = 1000, n_samples = 10, n_periods = 100, seed = 1)ELT= [51. 3. 3. 3. 3. 1. 1. 1. 1. 19. 19. 19. 19.]
S= [1348319.56810962 34742.07917634 16612.97028229 51290.49501161
53718.70272284 17130.14553439 8127.40124938 23756.17464127
3150.96049975 133232.97749839 64708.72283258 220679.57299807
234805.54429147]
t: Cost |dC| S
0: 220675718.04, 341808445420091.93750 [1348320.56810962 34743.07917634 16613.97028229 51289.49501161
53717.70272284 17131.14553439 8128.40124938 23757.17464127
3149.96049975 133231.97749839 64707.72283258 220680.57299807
234806.54429147]
50: 220518415.34, 745192019079272.87500 [1348369.74940509 34792.85221809 16664.8282914 51239.63768253
53667.72090384 17181.14553428 8178.40124932 23807.17464124
3099.97095921 133182.24568996 64657.06116374 220730.44691115
234856.53155207]
100: 220354712.04, 545116807024090.43750 [1348426.76713248 34846.91481195 16716.94689668 51187.45789964
53616.50062463 17231.14553417 8228.40124925 23857.17464121
3050.044785 133127.36879553 64603.34998017 220781.00090685
234905.83987621]
150: 220191360.04, 816167149409793.25000 [1348486.82370908 34903.48503105 16766.10557845 51133.51485836
53565.50242318 17277.19121652 8278.40124919 23907.17464117
3000.22634602 133069.85025368 64550.7454711 220832.68490125
234953.49107123]
200: 220031267.65, 524126465993651.37500 [1348542.95615425 34955.9460657 16815.80172057 51081.56513545
53514.01504129 17313.78270815 8327.85942526 23957.17398411
2950.52739226 133016.37778189 64498.76830765 220882.89683515
235002.88942521]
250: 219863018.77, 851656363689291.25000 [1348612.21089618 35006.21452572 16862.70239911 51027.50135256
53460.33050642 17351.19918629 8369.84554242 24007.15874206
2900.91843682 132960.78488283 64444.2078238 220930.75367586
235049.94351966]
300: 219700343.56, 491721644568249.31250 [1348676.41473432 35054.97028877 16909.60862722 50974.98279207
53408.28295656 17373.56656534 8411.73101577 24056.33644305
2851.52246168 132907.26589133 64390.73173766 220977.72557878
235095.97078381]
350: 219542527.16, 484599717516724.68750 [1348736.35266099 35102.34503693 16956.66288597 50924.01894217
53357.83028046 17396.07668408 8445.93033377 24105.04489955
2802.22025908 132855.793889 64338.46719159 221024.0100242
235141.25257648]
400: 219385962.74, 941456836707623.00000 [1348794.9972844 35150.88708824 17003.98943326 50872.34184194
53306.37285049 17420.11896177 8480.91118128 24152.88404331
2753.03918282 132803.81058383 64286.38134399 221071.74828293
235188.42507887]
450: 219231581.50, 1292884402927184.75000 [1348853.50496323 35195.70244227 17051.45155343 50820.34418959
53254.74315809 17445.57594705 8513.21949266 24200.89941181
2703.97199643 132754.33492422 64234.18980277 221119.93761815
235235.8310807 ]
500: 219077632.32, 518212719275614.12500 [1348911.93773799 35240.93227256 17097.03219103 50768.58804249
53203.15333844 17472.34115796 8538.87860671 24249.15353218
2654.8591634 132704.45854483 64183.09232032 221167.71096212
235283.11500071]
550: 218927945.80, 485300108160533.00000 [1348966.0166179 35285.31383805 17144.33879554 50718.35296326
53153.23104983 17500.32266857 8565.58203945 24297.48613848
2605.84288308 132656.52583678 64132.59678114 221215.37673921
235330.12264657]
600: 218785108.88, 564728180060374.50000 [1349018.55399569 35322.15998852 17187.18826913 50674.21697735
53110.22096048 17529.43982656 8593.41530842 24345.721259
2556.96370265 132614.06722426 64085.44475664 221254.63665692
235367.40000979]
650: 218646284.66, 231028727702383.43750 [1349070.90351672 35352.84581936 17226.14782567 50634.78730121
53072.46039344 17559.62092361 8622.31320316 24394.12631278
2508.00635225 132575.53572489 64040.66882231 221286.60962038
235396.3918021 ]
700: 218506805.66, 261632579367210.09375 [1349123.51945598 35385.14764584 17265.96791165 50594.24685425
53033.32750908 17590.80151025 8652.21613975 24442.68290959
2459.09382769 132535.61299023 63995.17601281 221319.80658156
235426.92666981]
750: 218369502.68, 256688191996597.75000 [1349175.01467117 35416.09715995 17305.43544488 50554.70182601
52995.33893496 17622.92314284 8683.06987149 24491.37060831
2410.33081751 132496.76185324 63950.27649986 221351.79321731
235455.93472848]
800: 218238726.74, 76741322279162.53125 [1349222.7074572 35442.901349 17340.43378657 50519.26270029
52961.25523777 17655.93243016 8714.82462737 24540.17268668
2361.73199689 132461.77924135 63909.55459394 221379.28820056
235480.69272982]
850: 218123687.56, 252671648888372.81250 [1349258.70671942 35462.56084521 17362.58570206 50493.34870657
52935.24328265 17689.78029324 8747.43444326 24589.07531308
2313.27083062 132435.63810722 63881.27524148 221398.5689691
235499.65316048]
900: 218009137.59, 68610489926442.88281 [1349294.39416997 35482.04231764 17384.15586794 50467.40216142
52909.2094108 17724.42138067 8780.85663644 24638.06691778
2264.76814395 132409.64951475 63853.40192051 221417.95847274
235518.71131709]
950: 217894318.98, 195265332282450.40625 [1349331.44805033 35501.08900369 17405.30090711 50440.96572054
52882.59493555 17759.81359948 8815.05138677 24687.13772632
2216.40572571 132383.31962837 63825.11154321 221437.14500597
235537.67686744]
Best: 217782429.64, 149495319804164.03125 [1349367.47399352 35517.50819437 17426.82285353 50416.49339415
52858.10594517 17794.46036713 8848.57052732 24732.04221619
2170.10604192 132358.93389869 63796.96827159 221453.67157211
235553.69765306]# stage_df = pd.read_csv(folder_bom + "ssa01.csv", index_col=0)
# bom_df = pd.read_csv(folder_bom + "ssa_bom01.csv", index_col=0)
# best_cost, stage_df, bom_df, fig = solve_SSA(stage_df, bom_df)
# cost, stage_df, I = periodic_inv_opt(stage_df, bom_df, max_iter = 1000, n_samples = 10, n_periods = 100, seed = 1)ELT= [13. 13. 43. 30. 25. 1. 1. 1.]
S= [ 4091.25968171 1573.2612339 18369.86692342 12870.65539681
10751.84569932 313.23453982 46.64485363 78.28970725]
t: Cost |dC| S
0: 738253.04, 1246180.05146 [ 4092.25968171 1574.2612339 18370.86692342 12871.65539681
10752.84569932 314.23453982 45.64485363 77.28970725]
50: 713359.98, 66398.11736 [ 4126.42972125 1582.6009784 18420.72971972 12921.39842509
10802.46119396 360.61652664 44.05167729 86.44553083]
100: 697639.86, 53830.07941 [ 4091.67521411 1584.22271517 18470.1237238 12968.54931585
10851.5716812 397.82352518 44.38684851 96.95976312]
150: 685425.19, 48819.45366 [ 4079.83481905 1586.63059694 18512.88671884 13015.14479448
10903.8863555 446.18484549 44.49041005 101.36175361]
200: 671502.46, 35828.72853 [ 4105.09263065 1588.59693178 18557.05478751 13057.59583735
10948.05285451 492.24195436 44.68381728 91.43024867]
250: 659084.98, 26829.23061 [ 4139.92605168 1589.98668442 18599.73444809 13096.62095046
10985.33379269 523.59614578 44.91317741 91.86145222]
300: 650148.26, 19159.74856 [ 4165.5160091 1591.75562153 18637.47297218 13130.09797031
11022.13602295 546.41056921 45.03762899 93.43725329]
350: 643304.81, 15687.78590 [ 4189.55033689 1592.70953476 18674.42229426 13160.04183158
11051.55120041 566.08940204 45.18650575 92.97595812]
400: 638532.00, 10794.45977 [ 4204.45349226 1593.43260336 18709.22350723 13191.90346841
11074.28284291 577.87592218 45.32749954 94.76898651]
450: 635303.54, 7460.30899 [ 4219.73677263 1594.94109142 18739.05818407 13218.34505493
11090.14206376 585.36319824 45.50282587 96.32977209]
500: 634971.64, 6489.75384 [ 4205.15995699 1594.66460962 18764.41560121 13242.9950394
11104.76389076 595.0605535 45.52592229 94.76459883]
550: 632963.55, 3295.00148 [ 4217.08463465 1596.33267547 18784.72278404 13262.46129873
11130.39204887 600.38535139 45.66693841 97.64674733]
600: 631952.77, 2317.41725 [ 4224.15853318 1596.71048501 18802.49007556 13277.91652818
11149.06447296 603.45915015 45.78075323 97.78152212]
650: 631286.34, 1530.61933 [ 4229.94756846 1597.52954626 18815.89877426 13292.54637619
11166.39287595 605.57515493 45.90637947 96.65280796]
700: 631066.34, 1517.05126 [ 4230.92904393 1597.63591293 18827.5361712 13307.72669112
11177.41762992 606.05643722 45.90453356 95.79483507]
750: 631333.14, 992.71457 [ 4226.21435871 1597.88033477 18840.39992139 13322.96803148
11187.32570124 606.11049996 45.94290883 95.9827774 ]
800: 630968.29, 666.99091 [ 4233.53446195 1598.39470045 18851.41302688 13334.88998105
11197.63796615 606.12822126 46.00327799 96.49321949]
850: 630994.24, 535.97391 [ 4235.19800183 1598.66085629 18862.17833695 13345.50332417
11205.21368173 606.3251161 46.08802725 96.52798901]
900: 631246.78, 650.50730 [ 4233.23452117 1598.47753639 18872.58430379 13354.65422521
11213.35212038 606.41638563 46.08940061 96.72492291]
950: 631469.82, 426.99272 [ 4232.59142704 1598.93457249 18881.19858988 13363.216574
11227.65568071 606.53896245 46.0892974 96.96500643]
Best: 631419.44, 363.69285 [ 4235.8734129 1599.09495873 18886.92290645 13373.24500118
11236.88720748 606.63677805 46.14271796 96.99789479]periodic_inv_opt_fit_one_cycle
periodic_inv_opt_fit_one_cycle (stage_df, bom_df, max_iter=1, n_samples=10, n_periods=100, seed=1, lr_find=False, max_lr=1.0, moms=(0.85, 0.95))
データフレームを入力とした定期発注方策最適化にfit_one_cycle法を適用
periodic_inv_opt_fit_one_cycle関数の使用例
# cost, stage_df, I, cost_list, phi_list = periodic_inv_opt_fit_one_cycle(stage_df, bom_df, max_iter = 1000, n_samples = 10,
# n_periods = 100, seed = 1, lr_find=False, max_lr =3., moms=(0.85,0.95))ELT= [13. 13. 43. 30. 25. 1. 1. 1.]
S= [ 4091.25968171 1573.2612339 18369.86692342 12870.65539681
10751.84569932 313.23453982 46.64485363 78.28970725]
t: Cost |dC| S
0: 738253.04, 1246180.05146 [ 4091.25968171 1573.2612339 18369.86692342 12870.65539681
10751.84569932 313.23453982 46.64485363 78.28970725]
50: 729962.63, 89221.59767 [ 4103.85176968 1579.8573079 18382.68942081 12883.48247112
10764.70974338 325.54292727 43.20516334 84.22070204]
100: 717473.79, 64478.15708 [ 4122.22831209 1582.4721447 18409.8506545 12910.6163079
10791.94966657 350.22769019 44.20632408 86.84664873]
150: 701812.48, 58172.65323 [ 4120.19269689 1584.16946547 18451.2273357 12951.53437628
10832.40539252 370.21700749 44.31117571 87.94913286]
200: 690953.13, 60815.35292 [ 4062.70653571 1585.69807974 18501.9607133 13000.27053152
10894.66454178 423.63561966 44.24871301 102.28241792]
250: 669454.27, 35903.22928 [ 4110.0131565 1589.35990371 18561.27325685 13063.44568125
10952.60156984 480.86736111 44.84719815 90.04694133]
300: 651959.38, 22369.98247 [ 4160.03111767 1590.95128037 18628.021709 13124.54412233
11010.7422393 527.18429571 44.96473601 93.08156545]
350: 640868.74, 14428.94592 [ 4188.07897284 1593.45999619 18697.3150612 13179.58213487
11068.59723696 553.86982831 45.29400135 93.93846431]
400: 634387.40, 6546.35564 [ 4219.32210446 1595.22121831 18758.49281169 13234.61171226
11097.53514323 568.46997814 45.53821725 95.20422733]
450: 631948.45, 2488.80843 [ 4225.03604559 1596.63585148 18802.02811649 13275.93793071
11146.58359853 577.4433366 45.77948835 98.02081483]
500: 631081.45, 1775.35928 [ 4230.42993272 1597.67066657 18831.48844513 13309.58154627
11180.65425739 574.25880735 45.90536989 95.88547543]
550: 630970.64, 617.93082 [ 4234.89376666 1598.45718056 18858.40419835 13338.65504692
11202.45543356 571.04654927 46.01808733 97.27355649]
600: 631544.47, 534.24797 [ 4230.62877671 1598.58264321 18881.2790734 13357.60957547
11221.70974986 570.3504795 46.07435167 98.29520824]
650: 631406.22, 337.12891 [ 4238.26664247 1599.30027922 18893.87019139 13375.21210064
11239.7887459 570.65236523 46.18509758 98.43290482]
700: 631465.29, 191.68175 [ 4241.63093738 1599.38044819 18902.08059305 13387.88206348
11249.01060311 571.435331 46.18127829 98.20658432]
750: 631534.94, 127.62068 [ 4243.77805685 1599.62032251 18908.61889896 13396.99837585
11255.72444415 572.09966484 46.25620134 97.39047516]
800: 631600.65, 106.00507 [ 4244.95997097 1599.74597316 18912.93543413 13402.38345209
11260.70871733 572.66442053 46.28662202 97.54121488]
850: 631596.31, 97.50065 [ 4246.6751567 1599.83671964 18915.27856784 13406.08338141
11263.49953519 573.02046203 46.30120998 97.53524439]
900: 631628.51, 99.24852 [ 4246.81121286 1599.8218352 18916.23618929 13408.21981863
11265.13857997 573.24120237 46.2968931 97.53178233]
950: 631648.49, 96.24211 [ 4246.69363253 1599.82581378 18916.60874107 13409.06371862
11265.84744558 573.32375665 46.29486373 97.53590301]
Best: 630910.88, 0.00965 [ 4234.58753372 1597.78313105 18826.26660408 13302.34402449
11175.91912062 574.98567419 45.92049737 96.15625735]# fig = plot_simulation(stage_df, I, n_periods =100, samples=5)
# plotly.offline.plot(fig);学習率探索の結果を可視化する関数 plot_inv_opt_lr_find
引数: - cost_list: 費用の変化を入れたリスト - ss_list: 学習率(ステップサイズ)設定のパラメータの変化を入れたリスト
返値: - Plotlyの図オブジェクト
plot_inv_opt_lr_find
plot_inv_opt_lr_find (cost_list, ss_list)
学習率探索の結果を可視化する関数
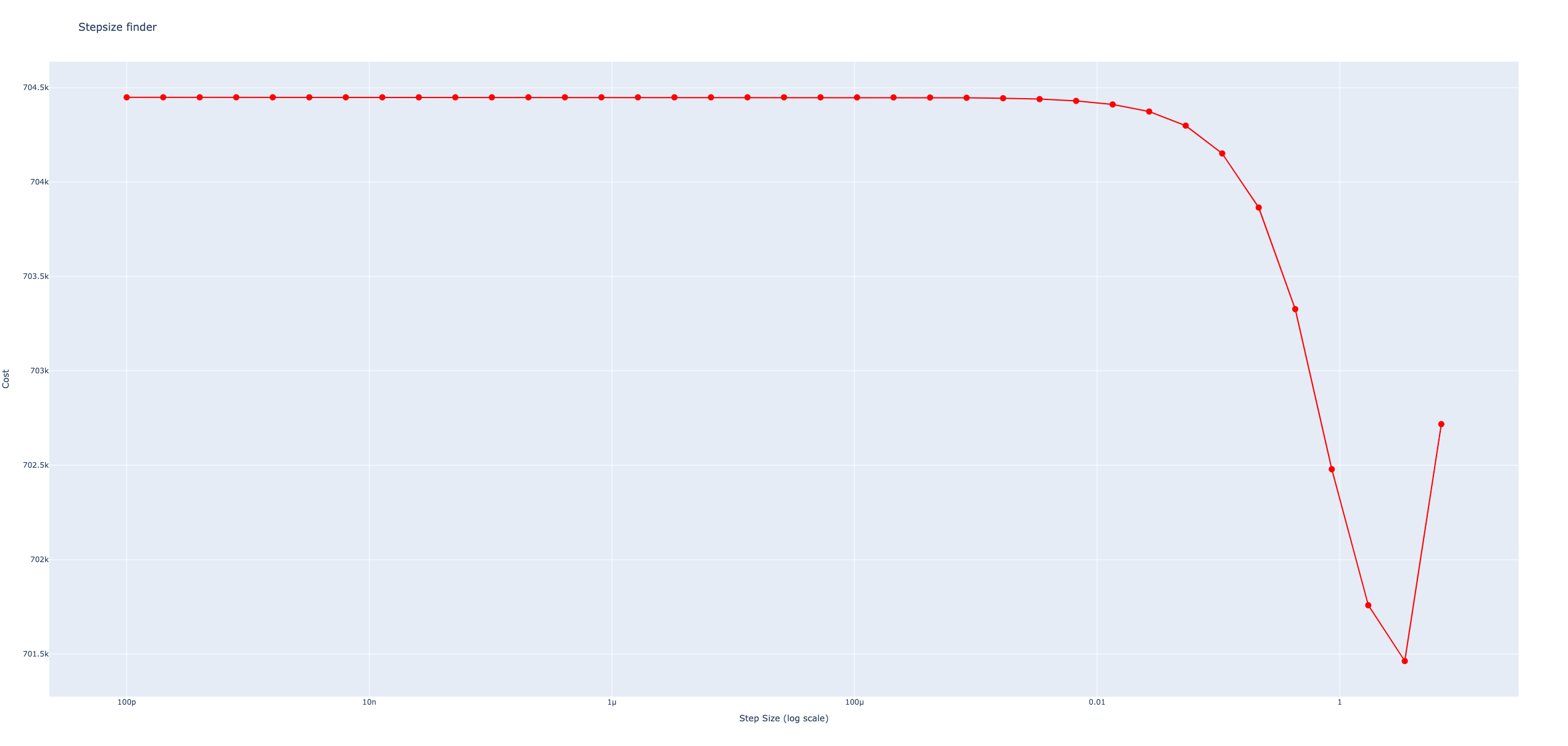
探索を可視化する関数 plot_inv_opt
引数: - cost_list: 費用の変化を入れたリスト
返値: - fig: 費用の変化を可視化した図オブジェクト
plot_inv_opt
plot_inv_opt (cost_list)
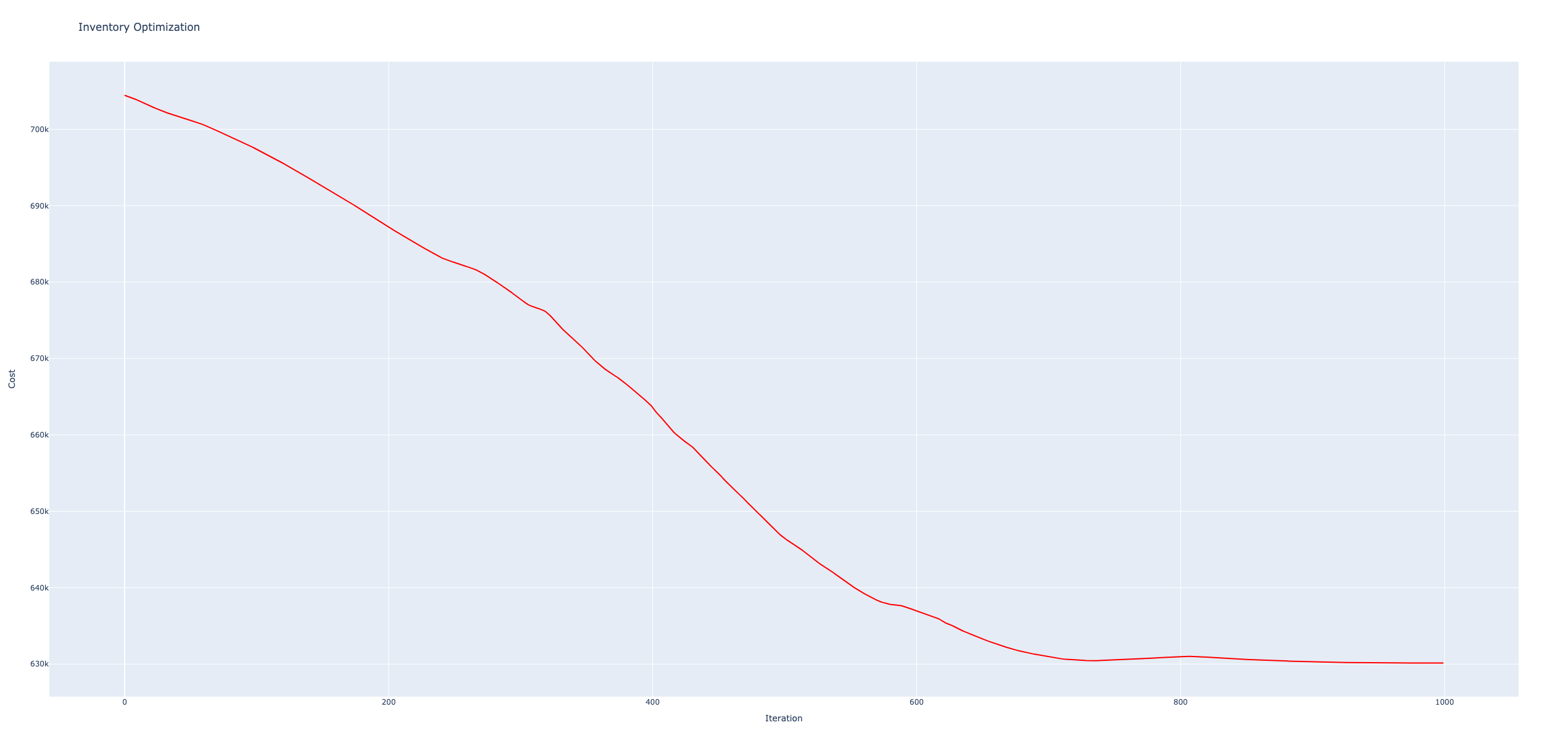
シミュレーション最適化の図表示関数 plot_simulation
plot_simulation
plot_simulation (stage_df, I, n_periods=1, samples=5, stage_id_list=None)
# fig = plot_simulation(stage_df, I, n_periods =100, samples=5)
# plotly.offline.plot(fig);