スケジューリング問題

スケジューリング問題に対する定式化とソルバー

準備

import random
import math
from gurobipy import Model, quicksum, GRB, multidict
#from mypulp import Model, quicksum, GRB,  multidict
#from mindoptpy import Model, quicksum, Column multidict
#from mindoptpy import MDO as GRB

スケジューリング問題

スケジューリング問題(scheduling problem)とは，稀少資源（機械）を諸活動（ジョブ，タスク，仕事，作業，オペレーションなどの総称）へ（時間軸を考慮して）割り振るための方法に対する理論体系である． スケジューリングの応用は，工場内での生産計画，計算機におけるジョブのコントロール，プロジェクトの遂行手順の決定など，様々である．

以下では，スケジューリングに関連する様々な数理・制約最適化による定式化とスケジューリングに特化したソルバーについて述べる．

1機械リリース時刻付き重み付き完了時刻和最小化問題

1機械リリース時刻付き重み付き完了時刻和最小化問題 \(1|r_j|\sum w_j C_j\) は，以下に定義される問題である．

単一の機械で \(n\) 個のジョブを処理する問題を考える． この機械は一度に1つのジョブしか処理できず，ジョブの処理を 開始したら途中では中断できないものと仮定する． ジョブの集合の添え字を \(j=1,2,\ldots,n\)，ジョブの集合を \(J=\{1,2,\ldots,n\}\) と書く． 各ジョブ\(j\) に対する処理時間 \(p_j\)，重要度を表す重み\(w_j\)， リリース時刻（ジョブの処理が開始できる最早時刻）\(r_j\)が与えられたとき， 各ジョブ \(j\) の処理完了時刻 \(C_j\) の重み付きの 和を最小にするようなジョブを機械にかける順番（スケジュール）を求めよ．

この問題は古くから多くの研究がなされているスケジューリング問題であり，\(NP\)-困難であることが知られている． ここでは，離接定式化(disjunctive formulation)と呼ばれる単純な定式化を示す．

ジョブ \(j\) の開始時刻を表す連続変数 \(s_{j}\) と，ジョブ \(j\) が他のジョブ \(k\) に先行する（前に処理される）とき \(1\) になる \(0\)-\(1\) 整数変数 \(x_{jk}\) を用いる．

離接定式化は，非常に大きな数 \(M\) を用いると，以下のように書ける．

\[ \begin{array}{l l l} minimize & \displaystyle\sum_{j=1}^n w_j s_{j} + \displaystyle\sum_{j=1}^n w_j p_j & \\ s.t. & s_j + p_j -M (1-x_{jk}) \leq s_k & \forall j \neq k \\ & x_{jk} +x _{kj}= 1 & \forall j < k \\ & s_j \geq r_j & \forall j=1,2,\ldots,n \\ & x_{jk} \in \{ 0,1 \} & \forall j \neq k \end{array} \]

目的関数は重み付き完了時刻の和 \(\sum w_j (s_j+p_j)\) を展開したものであり，それを最小化している． 展開した式の第2項は定数であるので，実際には第1項のみを最小化すれば良い． 最初の制約は，\(x_{jk}\) が \(1\) のとき，ジョブ\(j\) の完了時刻 \(s_j+p_j\) より ジョブ\(k\) の開始時刻 \(s_k\) が後になることを表す． （\(x_{jk}\) が \(0\) のときには，\(M\) が大きな数なので制約にはならない．） 2番目の制約は，ジョブ\(j\) がジョブ\(k\) に先行するか，ジョブ\(k\) がジョブ\(j\) に 先行するかの何れかが成立することを表す． これを離接制約(disjunctive constraint)と呼ぶ． これが離接定式化の名前の由来である． 3番目の制約は，ジョブ\(j\) の開始時刻 \(s_j\) がリリース時刻 \(r_j\) 以上であることを表す．

大きな数 \(M\) は，実際にはなるべく小さな値に設定すべきである． 制約ごとに異なる \(M\) を設定するならば，\(r_j +\sum s_j -s_k\)， すべての制約で同じ \(M\) を用いるならば \(\max (r_j) +\sum s_j\) とすれば十分である．

以下では，上の離接定式化を用いて5ジョブの例題を求解する．

def make_data(n):
    """
    Data generator for the one machine scheduling problem.
    """
    p, r, d, w = {}, {}, {}, {}

    J = range(1, n + 1)

    for j in J:
        p[j] = random.randint(1, 4)
        w[j] = random.randint(1, 3)

    T = sum(p)
    for j in J:
        r[j] = random.randint(0, 5)
        d[j] = r[j] + random.randint(0, 5)

    return J, p, r, d, w


def scheduling_disjunctive(J, p, r, w):
    """
    scheduling_disjunctive: model for the one machine total weighted completion time problem

    Disjunctive optimization model for the one machine total weighted
    completion time problem with release times.

    Parameters:
        - J: set of jobs
        - p[j]: processing time of job j
        - r[j]: earliest start time of job j
        - w[j]: weighted of job j,  the objective is the sum of the weighted completion time

    Returns a model, ready to be solved.
    """
    model = Model("scheduling: disjunctive")
    M = max(r.values()) + sum(p.values())  # big M
    s, x = (
        {},
        {},
    )  # start time variable, x[j,k] = 1 if job j precedes job k, 0 otherwise
    for j in J:
        s[j] = model.addVar(lb=r[j], vtype="C", name="s(%s)" % j)
        for k in J:
            if j != k:
                x[j, k] = model.addVar(vtype="B", name="x(%s,%s)" % (j, k))
    model.update()

    for j in J:
        for k in J:
            if j != k:
                model.addConstr(
                    s[j] - s[k] + M * x[j, k] <= (M - p[j]), "Bound(%s,%s)" % (j, k)
                )

            if j < k:
                model.addConstr(x[j, k] + x[k, j] == 1, "Disjunctive(%s,%s)" % (j, k))

    model.setObjective(quicksum(w[j] * s[j] for j in J), GRB.MINIMIZE)

    model.update()
    model.__data = s, x
    return model

n = 5  # number of jobs
random.seed(12)
J, p, r, d, w = make_data(n)

model = scheduling_disjunctive(J, p, r, w)
model.optimize()
s, x = model.__data
z = model.ObjVal + sum([w[j] * p[j] for j in J])
print("Opt.value by Disjunctive Formulation:", z)
seq = [j for (t, j) in sorted([(int(s[j].X + 0.5), j) for j in s])]
print("solition=", seq)

Set parameter Username
Academic license - for non-commercial use only - expires 2024-11-13
Gurobi Optimizer version 10.0.0 build v10.0.0rc2 (mac64[x86])

CPU model: Intel(R) Xeon(R) W-2140B CPU @ 3.20GHz
Thread count: 8 physical cores, 16 logical processors, using up to 16 threads

Optimize a model with 30 rows, 25 columns and 80 nonzeros
Model fingerprint: 0xa43763d2
Variable types: 5 continuous, 20 integer (20 binary)
Coefficient statistics:
  Matrix range     [1e+00, 2e+01]
  Objective range  [1e+00, 3e+00]
  Bounds range     [1e+00, 5e+00]
  RHS range        [1e+00, 2e+01]
Found heuristic solution: objective 66.0000000
Presolve removed 10 rows and 10 columns
Presolve time: 0.00s
Presolved: 20 rows, 15 columns, 60 nonzeros
Variable types: 5 continuous, 10 integer (10 binary)

Root relaxation: objective 2.700000e+01, 7 iterations, 0.00 seconds (0.00 work units)

    Nodes    |    Current Node    |     Objective Bounds      |     Work
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time

     0     0   27.00000    0    7   66.00000   27.00000  59.1%     -    0s
H    0     0                      56.0000000   27.00000  51.8%     -    0s
H    0     0                      55.0000000   27.00000  50.9%     -    0s
H    0     0                      53.0000000   49.42105  6.75%     -    0s
H    0     0                      52.0000000   49.42105  4.96%     -    0s
     0     0   51.00000    0    2   52.00000   51.00000  1.92%     -    0s

Cutting planes:
  Implied bound: 5
  MIR: 6
  Relax-and-lift: 1

Explored 1 nodes (31 simplex iterations) in 0.03 seconds (0.00 work units)
Thread count was 16 (of 16 available processors)

Solution count 5: 52 53 55 ... 66

Optimal solution found (tolerance 1.00e-04)
Best objective 5.200000000000e+01, best bound 5.200000000000e+01, gap 0.0000%
Opt.value by Disjunctive Formulation: 81.99999999999999
solition= [5, 1, 4, 2, 3]

OR-Toolsによるスケジューリングモデルの定式化

Googleが開発しているOR-Tools(cp-sat)を用いると，制約伝播を用いて最適解を出すことが可能である． OR-Toolsについての詳細は，以下を参照されたい．

https://developers.google.com/optimization

cp-satは制約最適化とよばれるパラダイムを用いて問題を記述する． 基本的な使用法については， 充足可能性問題と重み付き制約充足問題の章を参照されたい． ここでは，スケジューリングに特化した定式化の仕方を紹介する．

区間変数

ジョブ（タスク，活動）を表現するための変数として区間変数(interval variable)が準備されている． これは，モデルインスタンスのNewIntervalVarメソッドで生成される．引数は，開始時刻を表す整数変数（もしくは整数），作業時間を表す整数変数（もしくは整数）， 終了時刻を表す整数変数（もしくは整数）である．

以下の例では，0から100までの整数をとる開始・終了時刻変数と，定数10の作業時間をもつ区間変数を定義している．

from ortools.sat.python import cp_model

model = cp_model.CpModel()

start_var = model.NewIntVar(0, 100, 'start')
duration = 10  
end_var = model.NewIntVar(0, 100, 'end')
interval_var = model.NewIntervalVar(start_var, duration, end_var, 'interval')

interval_var

interval(start = start, size = 10, end = end)

重なり禁止制約

1機械を専有するジョブに対しては，重なり禁止制約が準備されている． これは，モデルインスタンスのAddNoOverlapメソッドで生成される． 引数は，区間変数のリストである．

以下の例では0から21日までの3週間を計画期間としたスケジューリング問題を考える． ジョブは0,1,2の3つであり，作業時間はそれぞれ3,4,5とする． 初日は月曜とし，週末の土日は仕事ができないことを表すために，開始・終了時刻を固定したダミーのジョブを準備する． また，ジョブ2とジョブ1の間には先行関係があると仮定する．これは，通常の線形制約として記述できる．

目的は最大完了時刻（メイクスパン）とする． 各ジョブの終了時刻の最大値をとる整数変数objを準備し，AddMaxEqualityメソッドで最大値と一致することを規定し，それを最小化する．

model = cp_model.CpModel()

horizon = 21  # 3 weeks

# job 0, duration 3
start_0 = model.NewIntVar(0, horizon, 'start_0')
duration_0 = 3  # Python cp/sat code accepts integer variables or constants.
end_0 = model.NewIntVar(0, horizon, 'end_0')
task_0 = model.NewIntervalVar(start_0, duration_0, end_0, 'job_0')

# job 1, duration 4
start_1 = model.NewIntVar(0, horizon, 'start_1')
duration_1 = 4  # Python cp/sat code accepts integer variables or constants.
end_1 = model.NewIntVar(0, horizon, 'end_1')
task_1 = model.NewIntervalVar(start_1, duration_1, end_1, 'job_1')

# job 2, duration 5
start_2 = model.NewIntVar(0, horizon, 'start_2')
duration_2 = 5  # Python cp/sat code accepts integer variables or constants.
end_2 = model.NewIntVar(0, horizon, 'end_2')
task_2 = model.NewIntervalVar(start_2, duration_2, end_2, 'job_2')

# Weekends
weekend_0 = model.NewIntervalVar(5, 2, 7, 'weekend_0')
weekend_1 = model.NewIntervalVar(12, 2, 14, 'weekend_1')
weekend_2 = model.NewIntervalVar(19, 2, 21, 'weekend_2')

# No Overlap constraint
model.AddNoOverlap([task_0, task_1, task_2, weekend_0, weekend_1, weekend_2])

#time constraint
model.Add(start_1 >= end_2)

# Makespan objective
obj = model.NewIntVar(0, horizon, 'makespan')
model.AddMaxEquality(obj, [end_0, end_1, end_2])
model.Minimize(obj)

solver = cp_model.CpSolver()
status = solver.Solve(model)

print('Optimal Schedule Length:', solver.ObjectiveValue())
print('Job 0 starts at ', solver.Value(start_0))
print('Job 1 starts at ', solver.Value(start_1))
print('Job 2 starts at ', solver.Value(start_2))

Optimal Schedule Length: 17.0
Job 0 starts at  14
Job 1 starts at  7
Job 2 starts at  0

OR-Toolsによる定式化と求解

OR-Tools(cp-sat)を用いて，1機械リリース時刻付き重み付き完了時刻和問題を解いてみる．

n = 5  # number of jobs
random.seed(12)
J, p, r, d, w = make_data(n)

model = cp_model.CpModel()

horizon = sum(p.values())+ max(r.values())
print("horizon=", horizon)

start, end, interval = {}, {}, {}
for j in J:
    start[j] = model.NewIntVar(r[j], horizon, f"start({j})")
    end[j] = model.NewIntVar(r[j]+p[j], horizon, f"end({j})")
    interval[j] = model.NewIntervalVar(start[j], p[j], end[j], f"job({j})")

model.AddNoOverlap([interval[j] for j in J])
model.Minimize(sum(w[j]*end[j] for j in J))

solver = cp_model.CpSolver()
status = solver.Solve(model)
print(solver.StatusName(status))
print('Optimal Schedule Length:', solver.ObjectiveValue())
for j in J:
    print(f'Job {j} starts at ', solver.Value(start[j]), r[j])

horizon= 22
OPTIMAL
Optimal Schedule Length: 82.0
Job 1 starts at  4 3
Job 2 starts at  11 4
Job 3 starts at  14 4
Job 4 starts at  8 5
Job 5 starts at  1 1

1機械総納期遅れ最小化問題

1機械総納期遅れ最小化問題 \(1||\sum T_j\) は，以下に定義される問題である．

単一の機械で \(n\) 個のジョブを処理する問題を考える． この機械は一度に1つのジョブしか処理できず，ジョブの処理を 開始したら途中では中断できないものと仮定する． ジョブの添え字を \(1,2,\ldots,n\) と書く． 各ジョブ\(j\) に対する 処理時間\(p_j\)，納期（ジョブが完了しなければならない時刻）\(d_j\)， が与えられたとき， 各ジョブ \(j\) の納期からの遅れの和（総納期遅れ）を 最小にするようなジョブを機械にかける順番（スケジュール）を求めよ．

この問題は，\(NP\)-困難であることが知られている． ここでは，大きな数 \(M\) を用いない定式化として線形順序付け定式化(linear ordering formulation)を考える．

ジョブ\(j\) の納期遅れを表す連続変数 \(T_{j}\)と，ジョブ\(j\) が他のジョブ\(k\) に先行する（前に処理される）とき \(1\) になる \(0\)-\(1\) 整数変数 \(x_{jk}\) を用いる．

上の記号を用いると，線形順序付け定式化は，以下のように書ける．

\[ \begin{array}{l l l} minimize & \displaystyle\sum_{j} w_j T_j & \\ s.t. & x_{jk} +x _{kj}= 1 & \forall j < k \\ & x_{jk}+x_{k \ell} +x_{\ell j} \leq 2 & \forall j \neq k \neq \ell \\ & \displaystyle\sum_{j=1}^n \displaystyle\sum_{k \neq j} p_k x_{kj} + p_j \leq d_j +T_j & \forall j=1,2,\ldots,n \\ & x_{jk} \in \{ 0,1 \} & \forall j \neq k \end{array} \]

上の定式化において， 目的関数は，各ジョブ \(j\) に対する納期遅れ \(T_j\) を重み \(w_j\) で乗じたものの和を 最小化することを表す．最初の制約は，ジョブ\(j\) がジョブ \(k\) の前に処理されるか， その逆にジョブ\(k\) がジョブ\(j\) の前に処理されるかのいずれかが成立することを表す． （ここまでは離接定式化と同じである．） 2番目の制約は，異なるジョブ\(j,k,\ell\) に対して， ジョブ\(j\) がジョブ\(k\) に先行， ジョブ\(k\) がジョブ\(\ell\) に先行， ジョブ\(\ell\) がジョブ\(j\) に先行の3つが同時に成り立つことがないことを表す． この2つの制約によって，ジョブ上に線形順序（ジョブが一列に並べられること）が規定される． これが線形順序付け定式化の名前の由来である． 3番目の制約は，変数 \(x\) で規定される順序付けと納期遅れを表す変数 \(T\) を繋ぐための 制約であり，ジョブ\(j\) の完了時刻が納期 \(d_j\) より超えている時間が納期遅れ \(T_j\) であることを規定する．

以下では，上の線形順序定式化を用いて5ジョブの例題を求解する．

def scheduling_linear_ordering(J, p, d, w):
    """
    scheduling_linear_ordering: model for the one machine total weighted tardiness problem

    Model for the one machine total weighted tardiness problem
    using the linear ordering formulation

    Parameters:
        - J: set of jobs
        - p[j]: processing time of job j
        - d[j]: latest non-tardy time for job j
        - w[j]: weighted of job j,  the objective is the sum of the weighted completion time

    Returns a model, ready to be solved.
    """
    model = Model("scheduling: linear ordering")

    T, x = {}, {}  # tardiness variable,  x[j,k] =1 if job j precedes job k, =0 otherwise
    for j in J:
        T[j] = model.addVar(vtype="C", name="T(%s)" % (j))
        for k in J:
            if j != k:
                x[j, k] = model.addVar(vtype="B", name="x(%s,%s)" % (j, k))
    model.update()

    for j in J:
        model.addConstr(
            quicksum(p[k] * x[k, j] for k in J if k != j) - T[j] <= d[j] - p[j],
            "Tardiness(%r)" % (j),
        )

        for k in J:
            if k <= j:
                continue
            model.addConstr(x[j, k] + x[k, j] == 1, "Disjunctive(%s,%s)" % (j, k))

            for ell in J:
                if ell > k:
                    model.addConstr(
                        x[j, k] + x[k, ell] + x[ell, j] <= 2,
                        "Triangle(%s,%s,%s)" % (j, k, ell),
                    )

    model.setObjective(quicksum(w[j] * T[j] for j in J), GRB.MINIMIZE)

    model.update()
    model.__data = x, T
    return model

n = 5  # number of jobs
random.seed(12)
J, p, r, d, w = make_data(n)

model = scheduling_linear_ordering(J, p, d, w)
model.optimize()
z = model.ObjVal
x, T = model.__data
for (i, j) in x:
    if x[i, j].X > 0.5:
        print("x(%s) = %s" % ((i, j), int(x[i, j].X + 0.5)))
for i in T:
    print("T(%s) = %s" % (i, int(T[i].X + 0.5)))
print("Opt.value by the linear ordering formulation=", z)

Gurobi Optimizer version 10.0.0 build v10.0.0rc2 (mac64[x86])

CPU model: Intel(R) Xeon(R) W-2140B CPU @ 3.20GHz
Thread count: 8 physical cores, 16 logical processors, using up to 16 threads

Optimize a model with 25 rows, 25 columns and 75 nonzeros
Model fingerprint: 0x00b1425c
Variable types: 5 continuous, 20 integer (20 binary)
Coefficient statistics:
  Matrix range     [1e+00, 4e+00]
  Objective range  [1e+00, 3e+00]
  Bounds range     [1e+00, 1e+00]
  RHS range        [1e+00, 6e+00]
Found heuristic solution: objective 36.0000000
Presolve removed 11 rows and 11 columns
Presolve time: 0.00s
Presolved: 14 rows, 14 columns, 50 nonzeros
Variable types: 0 continuous, 14 integer (10 binary)
Found heuristic solution: objective 35.0000000

Root relaxation: objective 1.966667e+01, 8 iterations, 0.00 seconds (0.00 work units)

    Nodes    |    Current Node    |     Objective Bounds      |     Work
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time

     0     0   19.66667    0    5   35.00000   19.66667  43.8%     -    0s
H    0     0                      25.0000000   19.66667  21.3%     -    0s
H    0     0                      23.0000000   19.66667  14.5%     -    0s
     0     0     cutoff    0        23.00000   23.00000  0.00%     -    0s

Cutting planes:
  MIR: 1
  Relax-and-lift: 1

Explored 1 nodes (14 simplex iterations) in 0.01 seconds (0.00 work units)
Thread count was 16 (of 16 available processors)

Solution count 4: 23 25 35 36 

Optimal solution found (tolerance 1.00e-04)
Best objective 2.300000000000e+01, best bound 2.300000000000e+01, gap 0.0000%
x((1, 2)) = 1
x((1, 3)) = 1
x((1, 4)) = 1
x((2, 3)) = 1
x((4, 2)) = 1
x((4, 3)) = 1
x((5, 1)) = 1
x((5, 2)) = 1
x((5, 3)) = 1
x((5, 4)) = 1
T(1) = 0
T(2) = 8
T(3) = 13
T(4) = 1
T(5) = 0
Opt.value by the linear ordering formulation= 23.0

OR-Toolsによる定式化と求解

OR-Tools(cp-sat)を用いて，1機械総納期遅れ最小化問題を解いてみる．

n = 5  # number of jobs
random.seed(12)
J, p, r, d, w = make_data(n)

model = cp_model.CpModel()

horizon = sum(p.values())
print("horizon=", horizon)

start, end, interval, tardiness = {}, {}, {}, {}
for j in J:
    start[j] = model.NewIntVar(0, horizon, f"start({j})")
    end[j] = model.NewIntVar(0, horizon, f"end({j})")
    interval[j] = model.NewIntervalVar(start[j], p[j], end[j], f"job({j})")
    tardiness[j] = model.NewIntVar(0, horizon, f"tardiness({j})")

model.AddNoOverlap([interval[j] for j in J])
for j in J:
    model.Add(end[j]-d[j] <= tardiness[j])
model.Minimize(sum(w[j]*tardiness[j] for j in J))

solver = cp_model.CpSolver()
status = solver.Solve(model)

print(solver.StatusName(status))
print('Optimal Schedule Length:', solver.ObjectiveValue())
for j in J:
    print(f'Job {j} ends at ', solver.Value(end[j]), solver.Value(tardiness[j]), d[j])

horizon= 17
OPTIMAL
Optimal Schedule Length: 23.0
Job 1 ends at  7 0 8
Job 2 ends at  13 8 5
Job 3 ends at  17 13 4
Job 4 ends at  10 1 9
Job 5 ends at  3 0 4

順列フローショップ問題

順列フローショップ問題(permutation flow shop problem) \(F|prmu|C_{\max}\)は，以下に定義される問題である．

\(n\) 個のジョブを\(m\)台の機械で順番に処理することを考える． この機械は一度に1つのジョブしか処理できず，ジョブの処理を 開始したら途中では中断できないものと仮定する． いま，各機械におけるジョブの処理順序が同一であるとしたとき， 最後の機械 \(m\) で最後に処理されるジョブの完了時刻を最小にする処理順を求めよ．

ここでは，この問題に対する位置データ定式化(positional data formulation) と呼ばれる定式化を示す．

いま，\(n\)個のジョブ（添え字は \(j\)）と \(m\)台の機械（添え字は \(i\)）があり， 各ジョブは，機械 \(1,2,\ldots,m\) の順番で処理されるものとする． （これがフローショップと呼ばれる所以である．） ジョブ\(j\) の機械\(i\) 上での処理時間を \(p_{ij}\) とする． ジョブの追い越しがないので，解はジョブの投入順序，いいかえれば順列で表現できる． （これが順列フローショップと呼ばれる所以である．） ジョブを並べたときの順番を \(\kappa\) で表すことにし，順番を表す変数 \(x_{j \kappa}\) を用いる．

\(x_{j \kappa}\)は，ジョブ \(j\) が \(\kappa\) 番目に投入されるとき \(1\) になる \(0\)-\(1\) 変数であり， \(s_{i \kappa}\)は，機械 \(i\) の \(\kappa\) 番目に並べられてるジョブの開始時刻を表す実数変数であり， \(f_{i \kappa}\)は，機械 \(i\) の \(\kappa\) 番目に並べられてるジョブの完了（終了）時刻を表す実数変数である．

この定式化は，ジョブ自身の開始時刻ではなく， 機械にかかるジョブの順番（位置）に対する開始時刻や終了時刻のデータを用いるので， 位置データ定式化と呼ばれる．

定式化は以下のようになる．

\[ \begin{array}{l l l} minimize & f_{m n} & \\ s.t. & \displaystyle\sum_{\kappa} x_{j\kappa} = 1 & \forall j=1,2,\ldots,n \\ & \displaystyle\sum_{j} x_{j\kappa} = 1 & \forall \kappa=1,2,\ldots,n \\ & f_{i \kappa} \leq s_{i,\kappa +1} & \forall i=1,2,\ldots,m, \kappa=1,2,\ldots,n-1 \\ & s_{i \kappa}+\displaystyle\sum_{j} p_{ij} x_{j \kappa} \leq f_{i \kappa} & \forall i=1,2,\ldots,m, \kappa=1,2,\ldots,n \\ & f_{i \kappa} \leq s_{i+1,\kappa} & \forall i=1,2,\ldots,m-1, \kappa=1,2,\ldots,n \\ & x_{j \kappa} \in \{ 0,1 \} & \forall j=1,2,\ldots,n, \kappa=1,2,\ldots,n \\ & s_{i \kappa} \geq 0 & \forall i=1,2,\ldots,m, \kappa=1,2,\ldots,n \\ & f_{i \kappa} \geq 0 & \forall i=1,2,\ldots,m, \kappa=1,2,\ldots,n \end{array} \]

上の定式化において， 目的関数は最後の機械(\(m\))の最後の（\(n\)番目の）ジョブの完了時刻 を最小化している． 最初の制約は，各ジョブがいずれかの位置（順番）に割り当てられることを表す． 2番目の制約は，各位置（場所）にいずれかのジョブが割り当てられることを表す． 3番目の制約は，\(\kappa\)番目のジョブの完了時刻より \(\kappa+1\)番目のジョブの開始時刻が 遅いことを表す． 4番目の制約は，機械\(i\) の \(\kappa\)番目のジョブの開始時刻と完了時刻の関係を 規定する制約であり， ジョブの位置を表す変数 \(x\) と開始（終了）時刻を表す変数 \(s\) (\(f\)) を繋ぐ制約である． これは，\(x_{j\kappa}\) が \(1\) のときに処理時間が \(p_{ij}\) になる ことから導かれる． 5番目の制約は，機械\(i\) 上で \(\kappa\)番目に割り当てられたジョブの完了時刻より， 機械\(i+1\) 上で \(\kappa\)番目に割り当てられたジョブの開始時刻が遅いことを表す．

以下では，ジョブ数 \(15\)，機械数 \(10\) の例題を求解する．

def permutation_flow_shop(n, m, p):
    """ permutation_flow_shop problem
    Parameters:
        - n: number of jobs
        - m: number of machines
        - p[i,j]: processing time of job i on machine j
    Returns a model, ready to be solved.
    """
    model = Model("permutation flow shop")
    x, s, f = {}, {}, {}
    for j in range(1, n + 1):
        for k in range(1, n + 1):
            x[j, k] = model.addVar(vtype="B", name="x(%s,%s)" % (j, k))

    for i in range(1, m + 1):
        for k in range(1, n + 1):
            s[i, k] = model.addVar(vtype="C", name="start(%s,%s)" % (i, k))
            f[i, k] = model.addVar(vtype="C", name="finish(%s,%s)" % (i, k))
    model.update()

    for j in range(1, n + 1):
        model.addConstr(
            quicksum(x[j, k] for k in range(1, n + 1)) == 1, "Assign1(%s)" % (j)
        )
        model.addConstr(
            quicksum(x[k, j] for k in range(1, n + 1)) == 1, "Assign2(%s)" % (j)
        )

    for i in range(1, m + 1):
        for k in range(1, n + 1):
            if k != n:
                model.addConstr(f[i, k] <= s[i, k + 1], "FinishStart(%s,%s)" % (i, k))
            if i != m:
                model.addConstr(f[i, k] <= s[i + 1, k], "Machine(%s,%s)" % (i, k))

            model.addConstr(
                s[i, k] + quicksum(p[i, j] * x[j, k] for j in range(1, n + 1))
                <= f[i, k],
                "StartFinish(%s,%s)" % (i, k),
            )

    model.setObjective(f[m, n], GRB.MINIMIZE)

    model.update()
    model.__data = x, s, f
    return model


def make_data_permutation_flow_shop(n, m):
    """make_data: prepare matrix of m times n random processing times"""
    p = {}
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            p[i, j] = random.randint(1, 10)
    return p

n = 15
m = 10
p = make_data_permutation_flow_shop(n, m)

model = permutation_flow_shop(n, m, p)
model.optimize()
x, s, f = model.__data
print("Opt.value=", model.ObjVal)

Gurobi Optimizer version 9.1.1 build v9.1.1rc0 (mac64)
Thread count: 8 physical cores, 16 logical processors, using up to 16 threads
Optimize a model with 455 rows, 525 columns and 3550 nonzeros
Model fingerprint: 0xbc9b34f3
Variable types: 300 continuous, 225 integer (225 binary)
Coefficient statistics:
  Matrix range     [1e+00, 1e+01]
  Objective range  [1e+00, 1e+00]
  Bounds range     [1e+00, 1e+00]
  RHS range        [1e+00, 1e+00]
Presolve removed 48 rows and 49 columns
Presolve time: 0.01s
Presolved: 407 rows, 476 columns, 3170 nonzeros
Variable types: 229 continuous, 247 integer (225 binary)

Root relaxation: objective 1.236138e+02, 1043 iterations, 0.04 seconds

    Nodes    |    Current Node    |     Objective Bounds      |     Work
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time

     0     0  123.61383    0  112          -  123.61383      -     -    0s
H    0     0                     158.0000000  123.61383  21.8%     -    0s
H    0     0                     155.0000000  123.61383  20.2%     -    0s
     0     0  123.95833    0  114  155.00000  123.95833  20.0%     -    0s
     0     0  123.99812    0  114  155.00000  123.99812  20.0%     -    0s
     0     0  124.00981    0  114  155.00000  124.00981  20.0%     -    0s
     0     2  124.03088    0  114  155.00000  124.03088  20.0%     -    0s
H   78    93                     151.0000000  124.47625  17.6%   179    0s
H   85    93                     149.0000000  124.47625  16.5%   172    0s
*  182   168              18     148.0000000  124.54493  15.8%   122    0s
H  223   201                     146.0000000  124.54493  14.7%   118    0s
H  377   285                     145.0000000  124.85476  13.9%   100    0s
H  380   285                     142.0000000  124.85476  12.1%   100    0s
  6177  2050  129.00000   28   56  142.00000  128.30382  9.65%  61.7    5s
*35346 11391              65     141.0000000  136.27130  3.35%  43.9    9s
 40739 12736  139.82068   59   34  141.00000  136.74569  3.02%  42.3   10s
 42407 13177  138.92099   57   53  141.00000  136.89366  2.91%  41.9   15s
*50385  9787              43     140.0000000  137.31864  1.92%  40.4   15s
 85349  4252     cutoff   32       140.00000  139.00000  0.71%  37.1   20s

Cutting planes:
  Gomory: 4
  MIR: 16
  Flow cover: 14

Explored 94493 nodes (3386238 simplex iterations) in 20.96 seconds
Thread count was 16 (of 16 available processors)

Solution count 10: 140 141 142 ... 158

Optimal solution found (tolerance 1.00e-04)
Best objective 1.400000000000e+02, best bound 1.400000000000e+02, gap 0.0000%
Opt.value= 140.0

ジョブショップスケジューリング問題

ジョブショップスケジューリング問題 \(J| | C_{\max}\) は，以下のように定義される古典的なスケジューリング問題である．

ジョブを \(J_1, J_2,\cdots, J_n\)， ジョブ \(J_j\) に属するオペレーションを \(O_{1j},O_{2j},\cdots,O_{m_j j}\)， 機械を \(M_1,M_2, \cdots, M_m\) とする． オペレーションは \(O_{1j},O_{2j},\cdots,O_{m_j j}\) の順で処理されなければならず， オペレーション \(O_{ij}\) を処理するには機械 \(\mu_{ij}\) を作業時間 \(p_{ij}\) だけ占有する． オペレーションが途中で中断できないという仮定の下で， 最後のオペレーションが完了する時刻を最小化する各機械上でのオペレーションの処理順序を求める問題．

OptSeqによる求解

この問題は 中規模な問題例でさえ数理最適化ソルバーで解くことは難しい． 実務的な付加条件のほとんどを考慮したスケジューリング最適化システムとしてOptSeqが開発されている． OptSeqについての詳細は，付録1を参照されたい．

ジョブショップスケジューリングのベンチマーク問題例も，OptSeqを使用すると比較的容易に良い解を得ることができる．

例として，以下のサイトから入手できるベンチマーク問題例を読み込んで解いてみよう．

• OR-Lib.: http://people.brunel.ac.uk/~mastjjb/jeb/orlib/jobshopinfo.html
• 多くのジョブショップスケジューリング問題例を含んだサイト: http://jobshop.jjvh.nl/

例としてft06.txtを用いる．このデータは，以下のテキストファイルである．

6 6
2  1  0  3  1  6  3  7  5  3  4  6
1  8  2  5  4 10  5 10  0 10  3  4
2  5  3  4  5  8  0  9  1  1  4  7
1  5  0  5  2  5  3  3  4  8  5  9 
2  9  1  3  4  5  5  4  0  3  3  1
1  3  3  3  5  9  0 10  4  4  2  1

得られた最大完了時刻 \(55\) は最適値である．

from optseq import *
# ジョブショップスケジューリング問題のベンチマーク問題例

fname = "../data/jssp/ft06.txt"
#fname = "../data/jssp/ta01.txt"

f = open(fname, "r")
lines = f.readlines()
f.close()
n, m = map(int, lines[0].split())
print("n,m=", n, m)

model = Model()
act, mode, res = {}, {}, {}
for j in range(m):
    res[j] = model.addResource(f"machine[{j}]", capacity=1)

# prepare data as dic
machine, proc_time = {}, {}
for i in range(n):
    L = list(map(int, lines[i + 1].split()))
    for j in range(m):
        machine[i, j] = L[2 * j]
        proc_time[i, j] = L[2 * j + 1]

for i, j in proc_time:
    act[i, j] = model.addActivity(f"Act[{i}_{j}]")
    mode[i, j] = Mode(f"Mode[{i}_{j}]", proc_time[i, j])
    mode[i, j].addResource(res[machine[i, j]], 1)
    act[i, j].addModes(mode[i, j])

for i in range(n):
    for j in range(m - 1):
        model.addTemporal(act[i, j], act[i, j + 1])

model.Params.TimeLimit = 1
model.Params.Makespan = True
#model.Params.OutputFlag = True
model.optimize()

n,m= 6 6

 ================ Now solving the problem ================ 


Solutions:
    source   ---     0     0
      sink   ---    55    55
  Act[0_0]   ---     5     6
  Act[0_1]   ---     6     9
  Act[0_2]   ---    16    22
  Act[0_3]   ---    30    37
  Act[0_4]   ---    42    45
  Act[0_5]   ---    49    55
  Act[1_0]   ---     0     8
  Act[1_1]   ---     8    13
  Act[1_2]   ---    13    23
  Act[1_3]   ---    28    38
  Act[1_4]   ---    38    48
  Act[1_5]   ---    48    52
  Act[2_0]   ---     0     5
  Act[2_1]   ---     5     9
  Act[2_2]   ---     9    17
  Act[2_3]   ---    18    27
  Act[2_4]   ---    27    28
  Act[2_5]   ---    42    49
  Act[3_0]   ---     8    13
  Act[3_1]   ---    13    18
  Act[3_2]   ---    22    27
  Act[3_3]   ---    27    30
  Act[3_4]   ---    30    38
  Act[3_5]   ---    45    54
  Act[4_0]   ---    13    22
  Act[4_1]   ---    22    25
  Act[4_2]   ---    25    30
  Act[4_3]   ---    38    42
  Act[4_4]   ---    48    51
  Act[4_5]   ---    52    53
  Act[5_0]   ---    13    16
  Act[5_1]   ---    16    19
  Act[5_2]   ---    19    28
  Act[5_3]   ---    28    38
  Act[5_4]   ---    38    42
  Act[5_5]   ---    42    43

#可視化
import plotly.express as px
import pandas as pd
import datetime as dt

start="2022/1/1"
period="days"

start = pd.to_datetime(start)

def time_convert_long(periods):
    if period =="days":
        time_ = start + dt.timedelta(days=float(periods))
    elif period == "hours":
        time_ = start + dt.timedelta(hours=float(periods))
    elif period == "minutes":
        time_ = start + dt.timedelta(minutes=float(periods))
    elif period == "seconds":
        time_ = start + dt.timedelta(seconds=float(periods))
    else:
        raise TypeError("pariod must be 'days' or 'seconds' or minutes' or 'days'")
    return time_.strftime("%Y-%m-%d")

L=[]
for i, j in proc_time:
    a = act[i,j]
    res = None
    for r in a.modes[0].requirement:  
        res = r[0]
        break
    st = time_convert_long(a.start)
    fi = time_convert_long(a.completion)
    L.append(dict(Task=a.name, Start=st, Finish=fi, Resource=res, Job= f"Job{i}" ) )
    
df = pd.DataFrame(L)
fig = px.timeline(df, x_start="Start", x_end="Finish", y="Resource", color="Job", opacity=0.5)
plotly.offline.plot(fig);

OR-Toolsを用いた求解

fname = "../data/jssp/ft06.txt"
#fname = "../data/jssp/ta01.txt"
#fname = "../data/jssp/ta21.txt"
f = open(fname, "r")
lines = f.readlines()
f.close()
n, m = map(int, lines[0].split())
print("n,m=", n, m)

# prepare data
machine, proc_time = {}, {}
for i in range(n):
    L = list(map(int, lines[i + 1].split()))
    for j in range(m):
        machine[i, j] = L[2 * j]
        proc_time[i, j] = L[2 * j + 1]
jobs_data = []
for i in range(n):
    row = []
    for j in range(m):
        row.append((machine[i, j], proc_time[i, j]))
    jobs_data.append(row)

n,m= 6 6

import collections
from ortools.sat.python import cp_model

model = cp_model.CpModel()

machines_count = 1 + max(task[0] for job in jobs_data for task in job)
all_machines = range(machines_count)

# Computes horizon dynamically as the sum of all durations.
horizon = sum(task[1] for job in jobs_data for task in job)

# Named tuple to store information about created variables
task_type = collections.namedtuple("task_type", "start end interval")
# Named tuple to manipulate solution information
assigned_task_type = collections.namedtuple(
    "assigned_task_type", "start job index duration"
)

# Creates job intervals and add to the corresponding machine lists
all_tasks = {}
machine_to_intervals = collections.defaultdict(list)

for job_id, job in enumerate(jobs_data):
    for task_id, task in enumerate(job):
        machine = task[0]
        duration = task[1]
        suffix = "_%i_%i" % (job_id, task_id)
        start_var = model.NewIntVar(0, horizon, "start" + suffix)
        end_var = model.NewIntVar(0, horizon, "end" + suffix)
        interval_var = model.NewIntervalVar(
            start_var, duration, end_var, "interval" + suffix
        )
        all_tasks[job_id, task_id] = task_type(
            start=start_var, end=end_var, interval=interval_var
        )
        machine_to_intervals[machine].append(interval_var)

# Create and add disjunctive constraints
for machine in all_machines:
    model.AddNoOverlap(machine_to_intervals[machine])

# Precedences inside a job
for job_id, job in enumerate(jobs_data):
    for task_id in range(len(job) - 1):
        model.Add(
            all_tasks[job_id, task_id + 1].start >= all_tasks[job_id, task_id].end
        )

# Makespan objective
obj_var = model.NewIntVar(0, horizon, "makespan")
model.AddMaxEquality(
    obj_var,
    [all_tasks[job_id, len(job) - 1].end for job_id, job in enumerate(jobs_data)],
)
model.Minimize(obj_var)

# Solve model
solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = 360.0
status = solver.Solve(model)


# Create one list of assigned tasks per machine.
assigned_jobs = collections.defaultdict(list)
for job_id, job in enumerate(jobs_data):
    for task_id, task in enumerate(job):
        machine = task[0]
        assigned_jobs[machine].append(
            assigned_task_type(
                start=solver.Value(all_tasks[job_id, task_id].start),
                job=job_id,
                index=task_id,
                duration=task[1],
            )
        )

# Create per machine output lines.
output = ""
for machine in all_machines:
    # Sort by starting time.
    assigned_jobs[machine].sort()
    sol_line_tasks = "Machine " + str(machine) + ": "
    sol_line = "           "

    for assigned_task in assigned_jobs[machine]:
        name = "job_%i_%i" % (assigned_task.job, assigned_task.index)
        # Add spaces to output to align columns.
        sol_line_tasks += "%-10s" % name

        start = assigned_task.start
        duration = assigned_task.duration
        sol_tmp = "[%i,%i]" % (start, start + duration)
        # Add spaces to output to align columns.
        sol_line += "%-10s" % sol_tmp

    sol_line += "\n"
    sol_line_tasks += "\n"
    output += sol_line_tasks
    output += sol_line

# Finally print the solution found.
print("Optimal Schedule Length: %i" % solver.ObjectiveValue())
print(output)

Optimal Schedule Length: 55
Machine 0: job_0_1   job_3_1   job_2_3   job_5_3   job_1_4   job_4_4   
           [1,4]     [13,18]   [19,28]   [28,38]   [38,48]   [48,51]   
Machine 1: job_1_0   job_3_0   job_5_0   job_0_2   job_4_1   job_2_4   
           [0,8]     [8,13]    [13,16]   [16,22]   [22,25]   [41,42]   
Machine 2: job_0_0   job_2_0   job_1_1   job_4_0   job_3_2   job_5_5   
           [0,1]     [2,7]     [8,13]    [13,22]   [22,27]   [42,43]   
Machine 3: job_2_1   job_5_1   job_3_3   job_0_3   job_1_5   job_4_5   
           [7,11]    [16,19]   [27,30]   [30,37]   [48,52]   [52,53]   
Machine 4: job_1_2   job_4_2   job_3_4   job_5_4   job_0_5   job_2_5   
           [13,23]   [25,30]   [30,38]   [38,42]   [42,48]   [48,55]   
Machine 5: job_2_2   job_5_2   job_1_3   job_0_4   job_4_3   job_3_5   
           [11,19]   [19,28]   [28,38]   [38,41]   [41,45]   [45,54]   

数理最適化ソルバーを用いた求解

数理最適化による定式化も可能である． 以下では，次の資源制約付きプロジェクトスケジューリング問題で導入する時刻添え字定式化と， 1機械リリース時刻付き完了時刻和最小化問題で用いた離接定式化による求解を試みる．

ここでは，各ジョブに含まれるオペレーション数が機械の数 \(m\) に一致するものと仮定する． オペレーションをジョブと順序の組として \((i,j)\) もしくは \((k,l)\) と書く．

ジョブショップスケジューリング問題は資源制約付きプロジェクトスケジューリング問題の特殊形であるので，時刻添え字定式化は省略する．

離接定式化では， オペレーション \((i,j)\) の開始時刻を表す連続変数 \(s_{ij}\) と， オペレーション \((i,j)\) が他のオペレーション \((k,l)\) に先行する（前に処理される）とき \(1\) になる \(0\)-\(1\) 整数変数 \(x_{ijkl}\) を用いる． また，最大完了時刻を表す実数変数を \(z\) とする．

非常に大きな数 \(M\) を用いると，離散定式化は以下のように書ける．

\[ \begin{array}{l l l} minimize & z & \\ s.t. & s_{ij} + p_{ij} -M (1-x_{ijkl}) \leq s_{kl} & \forall j \neq k \\ & x_{ijkl} +x _{klij}= 1 & \forall (i,j) < (k,l) \\ & s_{ij} + p_{ij} \leq s_{i,j+1} & \forall i, j=1,\ldots,m-1 \\ & s_{im} \leq z & \forall i \\ & s_{i1} \geq 0 & \forall i \\ & x_{ijkl} \in \{ 0,1 \} & \forall (i,j) \neq (k,l) \end{array} \]

fname = "../data/jssp/ft06.txt"
# fname = "../data/jssp/ta21.txt"
f = open(fname, "r")
lines = f.readlines()
f.close()
n, m = map(int, lines[0].split())
print("n,m=", n, m)

machine, proc_time = {}, {}
for i in range(n):
    L = list(map(int, lines[i + 1].split()))
    for j in range(m):
        machine[i, j] = L[2 * j]
        proc_time[i, j] = L[2 * j + 1]

n,m= 6 6

# 時刻添え字定式化
from gurobipy import Model, GRB, quicksum

model = Model("scheduling: time-index")
T = 55  # メイクスパン以上の計画期間

s, x = {}, {}  # s - start time variable,   x=1 if job (i,j) starts at period t
for i, j in proc_time:
    s[i, j] = model.addVar(vtype="C", name=f"s({i},{j})")
    for t in range(1, T - proc_time[i, j] + 2):
        x[i, j, t] = model.addVar(vtype="B", name=f"x({i},{j},{t})")
z = model.addVar(vtype="C", name="z")  # completion time
model.update()

for i, j in proc_time:
    # job execution constraints
    model.addConstr(
        quicksum(x[i, j, t] for t in range(1, T - proc_time[i, j] + 2)) == 1
    )

    # start time constraints
    model.addConstr(
        quicksum((t - 1) * x[i, j, t] for t in range(2, T - proc_time[i, j] + 2))
        == s[i, j]
    )

# resource upper bound constraints
for t in range(1, T + 1):
    for k in range(m):  # machine
        model.addConstr(
            quicksum(
                x[i, j, t_]
                for i, j in proc_time
                if machine[i, j] == k
                for t_ in range(
                    max(t - proc_time[i, j] + 1, 1), min(t + 1, T - proc_time[i, j] + 2)
                )
            )
            <= 1
        )

# time (precedence) constraints, i.e., s[k]-s[j] >= p[j]
for i in range(n):
    for j in range(m - 1):
        model.addConstr(s[i, j] + proc_time[i, j] <= s[i, j + 1])
    model.addConstr(s[i, m - 1] + proc_time[i, m - 1] <= z)

model.setObjective(z, GRB.MINIMIZE)
model.optimize()

Set parameter Username
Academic license - for non-commercial use only - expires 2023-11-07
Gurobi Optimizer version 9.5.2 build v9.5.2rc0 (mac64[x86])
Thread count: 8 physical cores, 16 logical processors, using up to 16 threads
Optimize a model with 438 rows, 1856 columns and 13375 nonzeros
Model fingerprint: 0x81d78eef
Variable types: 37 continuous, 1819 integer (1819 binary)
Coefficient statistics:
  Matrix range     [1e+00, 5e+01]
  Objective range  [1e+00, 1e+00]
  Bounds range     [1e+00, 1e+00]
  RHS range        [1e+00, 1e+01]
Presolve removed 108 rows and 1160 columns
Presolve time: 0.03s
Presolved: 330 rows, 696 columns, 4424 nonzeros
Variable types: 0 continuous, 696 integer (665 binary)

Root relaxation: objective 4.955932e+01, 325 iterations, 0.01 seconds (0.00 work units)

    Nodes    |    Current Node    |     Objective Bounds      |     Work
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time

     0     0   49.55932    0  105          -   49.55932      -     -    0s
     0     0   50.37220    0  146          -   50.37220      -     -    0s
     0     0   50.37507    0  146          -   50.37507      -     -    0s
     0     0   50.37507    0  152          -   50.37507      -     -    0s
     0     0   51.83488    0  168          -   51.83488      -     -    0s
     0     0   52.09226    0  170          -   52.09226      -     -    0s
     0     0   52.09238    0  171          -   52.09238      -     -    0s
     0     0   53.31236    0  169          -   53.31236      -     -    0s
     0     0   53.39541    0  160          -   53.39541      -     -    0s
     0     0   53.42883    0  155          -   53.42883      -     -    0s
H    0     0                      55.0000000   53.84137  2.11%     -    0s
     0     0     cutoff    0        55.00000   55.00000  0.00%     -    0s

Cutting planes:
  Cover: 7
  Implied bound: 2
  Clique: 41
  MIR: 20
  StrongCG: 4
  GUB cover: 37
  Zero half: 21
  RLT: 5
  Relax-and-lift: 6

Explored 1 nodes (3003 simplex iterations) in 0.34 seconds (0.23 work units)
Thread count was 16 (of 16 available processors)

Solution count 1: 55 

Optimal solution found (tolerance 1.00e-04)
Best objective 5.500000000000e+01, best bound 5.500000000000e+01, gap 0.0000%

#離接定式化
from gurobipy import Model, GRB, quicksum

model = Model("scheduling: disjunctive")
M = 3000  # big M
s, x = {}, {}  # start time variable, x[i,j,k,l] = 1 if job (i,j) precedes job (k,l), 0 otherwise
for i,j in proc_time:
    s[i,j] = model.addVar(vtype="C", name= f"s({i},{j})")
    for k,l in proc_time:
        if machine[i,j]==machine[k,l] and (i,j) != (k,l):
            x[i, j, k, l] = model.addVar(vtype="B", ub=1., name= f"x({i},{j},{k},{l})")
z = model.addVar(vtype="C", name= "z" ) #completion time
model.update()

for i,j in proc_time:
    for k,l in proc_time:
        if machine[i,j]==machine[k,l] and (i,j) != (k,l):
            model.addConstr(
                s[i,j] - s[k,l] + M * x[i, j, k, l] <= M - proc_time[i,j]
            )
        if machine[i,j]==machine[k,l] and (i,j) < (k,l):
            model.addConstr(x[i,j,k,l] + x[k,l,i,j] == 1)
                
for i in range(n):
    for j in range(m-1):
        model.addConstr(s[i,j] +proc_time[i,j] <=  s[i,j+1])
        
    model.addConstr(s[i,m-1]+ proc_time[i,m-1] <=z  )
    
model.setObjective(z, GRB.MINIMIZE)

model.Params.LogFile = "gurobi_jssp.log"
model.Params.TimeLimit = 60
model.Params.OutputFlag = 1
model.optimize()

#パラメータチューニング
# model.Params.TuneTimeLimit = 3600
# model.Params.TuneCriterion = 2 # best feasible solution found.
# model.tune()

Set parameter LogFile to value "gurobi_jssp.log"
Set parameter TimeLimit to value 60
Gurobi Optimizer version 9.5.2 build v9.5.2rc0 (mac64[x86])
Thread count: 8 physical cores, 16 logical processors, using up to 16 threads
Optimize a model with 306 rows, 217 columns and 792 nonzeros
Model fingerprint: 0xe048963c
Variable types: 37 continuous, 180 integer (180 binary)
Coefficient statistics:
  Matrix range     [1e+00, 3e+03]
  Objective range  [1e+00, 1e+00]
  Bounds range     [1e+00, 1e+00]
  RHS range        [1e+00, 3e+03]
Presolve removed 90 rows and 90 columns
Presolve time: 0.00s
Presolved: 216 rows, 127 columns, 612 nonzeros
Variable types: 37 continuous, 90 integer (90 binary)
Found heuristic solution: objective 170.0000000

Root relaxation: objective 4.700000e+01, 61 iterations, 0.00 seconds (0.00 work units)

    Nodes    |    Current Node    |     Objective Bounds      |     Work
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time

     0     0   47.00000    0   10  170.00000   47.00000  72.4%     -    0s
H    0     0                      73.0000000   47.00000  35.6%     -    0s
H    0     0                      60.0000000   47.00000  21.7%     -    0s
     0     0   47.00000    0   11   60.00000   47.00000  21.7%     -    0s
H    0     0                      58.0000000   47.00000  19.0%     -    0s
     0     0   47.00000    0   12   58.00000   47.00000  19.0%     -    0s
     0     0   47.00000    0   12   58.00000   47.00000  19.0%     -    0s
     0     0   47.00299    0   18   58.00000   47.00299  19.0%     -    0s
H    0     0                      57.0000000   47.00299  17.5%     -    0s
H    0     0                      56.0000000   50.00000  10.7%     -    0s
     0     0   50.00000    0    5   56.00000   50.00000  10.7%     -    0s
H    0     0                      55.0000000   50.00000  9.09%     -    0s
     0     0   50.00000    0    7   55.00000   50.00000  9.09%     -    0s
     0     0   50.00000    0    8   55.00000   50.00000  9.09%     -    0s
     0     0 infeasible    0        55.00000   55.00000  0.00%     -    0s

Explored 1 nodes (568 simplex iterations) in 0.07 seconds (0.02 work units)
Thread count was 16 (of 16 available processors)

Solution count 9: 55 55 55 ... 170

Optimal solution found (tolerance 1.00e-04)
Best objective 5.499999999440e+01, best bound 5.499999999440e+01, gap 0.0000%

#目的関数値の変化
import grblogtools as glt

results = glt.parse(model.Params.LogFile)
summary = results.summary()
nodelog_progress = results.progress("nodelog")
nodelog_progress.Incumbent.plot()
nodelog_progress.BestBd.plot();

#summary.T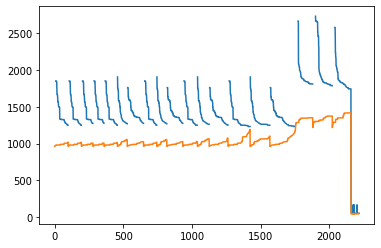

資源制約付きプロジェクトスケジューリング問題

様々なスケジューリング問題を一般化した，以下の資源制約付き（プロジェクト）スケジューリング問題を考える．

ジョブの集合 \(Job\) ， 各時間ごとの使用可能量の上限をもつ資源 \(Res\) が与えられている． 資源は，ジョブごとに決められた作業時間の間はジョブによって使用されるが， 作業完了後は，再び使用可能になる． ジョブ間に与えられた時間制約を満たした上で， ジョブの作業開始時刻に対する任意の関数の和を最小化するような， 資源のジョブへの割り振りおよびジョブの作業開始時刻を求める．

時刻を離散化した期の概念を用いた定式化（時刻添え字定式化）を示す．

まず，定式化で用いる集合，入力データ，変数を示す．

集合:

• \(Job\): ジョブの集合．添え字は \(j,k\)
• \(Res\): 資源の集合．添え字は \(r\)
• \(Prec\): ジョブ間の時間制約を表す集合． \(Job \times Job\) の部分集合で， \((j,k) \in Prec\) のとき， ジョブ \(j\) とジョブ \(k\) の開始（完了）時刻間に何らかの制約が定義されるものとする

入力データ:

• \(T\): 最大の期数．期の添え字は \(t=1,2,\ldots,T\)． 連続時間との対応づけは，時刻 \(t-1\) から \(t\) までを期 \(t\) と定義する． なお，期を表す添え字は \(t\) の他に \(s\) も用いる．
• \(p_j\): ジョブ \(j\) の処理時間．非負の整数を仮定
• \(Cost_{jt}\): ジョブ \(j\) を期\(t\) に開始したときの費用
• \(a_{jrt}\): ジョブ \(j\) の開始後 \(t(=0,1,\ldots,p_j-1)\)期経過時の処理に要する資源\(r\) の量
• \(RUB_{rt}\): 時刻 \(t\) における資源 \(r\) の使用可能量の上限

変数: - \(x_{jt}\): ジョブ \(j\) を時刻 \(t\) に開始するとき \(1\)，それ以外のとき \(0\) を表す \(0\)-\(1\)変数

以下に資源制約付きスケジューリング問題の定式化を示す．

• 目的関数: \[ minimize \sum_{j \in Job} \sum_{t=1}^{T-p_j+1} Cost_{jt} x_{jt} \]

• ジョブ遂行制約： \[ \sum_{t=1}^{T-p_j+1} x_{jt} =1　 \forall j \in Job \] すべてのジョブは必ず1度処理されなければならないことを表す．

• 資源制約：

\[ \sum_{j \in Job} \sum_{s =\max\{t-p_j+1,1\}}^{\min\{t,T-p_j+1\}} a_{jr,t-s} x_{js} \leq RUB_{rt} \ \ \ \forall r \in Res , t \in \{1,2,\ldots,T \} \]

ある時刻 \(t\) に作業中であるジョブの資源使用量の合計 が，資源使用量の上限を超えないことを規定する． 時刻 \(t\) に作業中であるジョブは， 時刻 \(t-p_j+1\) から \(t\) の間に作業を開始したジョブであるので，上式を得る．

• 時間制約：

ジョブ \(j\) の開始時刻 \(S_j\) は \(\sum_{t=2}^{T-p_j+1} (t-1)x_{jt}\) であるので， 完了時刻 \(C_j\) はそれに \(p_j\) を加えたものになる． ジョブの対 \((j,k) \in Prec\) に対しては，ジョブ \(j,k\) の開始（完了）時刻間に 何らかの制約が付加される．たとえば，ジョブ \(j\) の処理が終了するまで，ジョブ \(k\) の処理が開始できないことを表す先行制約は，

\[ \sum_{t=2}^{T-p_j+1} (t-1)x_{jt} +p_j \leq \sum_{t=2}^{T-p_k+1} (t-1) x_{kt}  \ \ \ \forall (j,k) \in Prec \]

と書くことができる． ここで，左辺の式は，ジョブ \(j\)の完了時刻を表し，右辺の式はジョブ \(k\) の開始時刻を表す．

以下に，数理最適化ソルバー Gurobiを用いたモデルを示す． 実際には，Gurobiでは中規模問題例までしか解くことができない． ジョブショップスケジューリング問題と同様に，OptSeqやOR-toolsを用いることによって求解できる．

ただし，実務の問題はさらなる付加条件がつくことが多い．OptSeqは，より一般的なスケジューリング問題をモデル化できるように設計されている．

from gurobipy import Model, quicksum, GRB, multidict
# from mypulp import Model, quicksum, GRB, multidict

def rcs(J, P, R, T, p, c, a, RUB):
    """rcs -- model for the resource constrained scheduling problem
    Parameters:
        - J: set of jobs
        - P: set of precedence constraints between jobs
        - R: set of resources
        - T: number of periods
        - p[j]: processing time of job j
        - c[j,t]: cost incurred when job j starts processing on period t.
        - a[j,r,t]: resource r usage for job j on period t (after job starts)
        - RUB[r,t]: upper bound for resource r on period t
    Returns a model, ready to be solved.
    """
    model = Model("resource constrained scheduling")
    s, x = {}, {}  # s - start time variable,   x=1 if job j starts on period t
    for j in J:
        s[j] = model.addVar(vtype="C", name="s(%s)" % j)
        for t in range(1, T - p[j] + 2):
            x[j, t] = model.addVar(vtype="B", name="x(%s,%s)" % (j, t))
    model.update()

    for j in J:
        # job execution constraints
        model.addConstr(
            quicksum(x[j, t] for t in range(1, T - p[j] + 2)) == 1,
            "ConstrJob(%s,%s)" % (j, t),
        )

        # start time constraints
        model.addConstr(
            quicksum((t - 1) * x[j, t] for t in range(2, T - p[j] + 2)) == s[j],
            "ConstrJob(%s,%s)" % (j, t),
        )

    # resource upper bound constraints
    for t in range(1, T+1):
        for r in R:
            model.addConstr(
                quicksum(
                    a[j, r, t - t_] * x[j, t_]
                    for j in J
                    for t_ in range(max(t - p[j] + 1, 1), min(t + 1, T - p[j] + 2))
                )
                <= RUB[r, t],
                "ResourceUB(%s,%s)" % (r,t)
            )

    # time (precedence) constraints, i.e., s[k]-s[j] >= p[j]
    for (j, k) in P:
        model.addConstr(s[k] - s[j] >= p[j], "Precedence(%s,%s)" % (j, k))

    model.setObjective(quicksum(c[j, t] * x[j, t] for (j, t) in x), GRB.MINIMIZE)

    model.update()
    model.__data = x, s
    return model


def make_1r():
    J, p = multidict(
        {  # jobs, processing times
            1: 1,
            2: 3,
            3: 2,
            4: 2,
        }
    )
    P = [(1, 2), (1, 3), (2, 4)]
    R = [1]
    T = 6
    c = {}
    for j in J:
        for t in range(1, T - p[j] + 2):
            c[j, t] = 1 * (t - 1 + p[j])
    a = {
        (1, 1, 0): 2,
        (2, 1, 0): 2,
        (2, 1, 1): 1,
        (2, 1, 2): 1,
        (3, 1, 0): 1,
        (3, 1, 1): 1,
        (4, 1, 0): 1,
        (4, 1, 1): 2,
    }
    RUB = {(1, 1): 2, (1, 2): 2, (1, 3): 1, (1, 4): 2, (1, 5): 2, (1, 6): 2}
    return (J, P, R, T, p, c, a, RUB)


def make_2r():
    J, p = multidict(
        {  # jobs, processing times
            1: 2,
            2: 2,
            3: 3,
            4: 2,
            5: 5,
        }
    )
    P = [(1, 2), (1, 3), (2, 4)]
    R = [1, 2]
    T = 6
    c = {}
    for j in J:
        for t in range(1, T - p[j] + 2):
            c[j, t] = 1 * (t - 1 + p[j])
    a = {
        # resource 1:
        (1, 1, 0): 2,
        (1, 1, 1): 2,
        (2, 1, 0): 1,
        (2, 1, 1): 1,
        (3, 1, 0): 1,
        (3, 1, 1): 1,
        (3, 1, 2): 1,
        (4, 1, 0): 1,
        (4, 1, 1): 1,
        (5, 1, 0): 0,
        (5, 1, 1): 0,
        (5, 1, 2): 1,
        (5, 1, 3): 0,
        (5, 1, 4): 0,
        # resource 2:
        (1, 2, 0): 1,
        (1, 2, 1): 0,
        (2, 2, 0): 1,
        (2, 2, 1): 1,
        (3, 2, 0): 0,
        (3, 2, 1): 0,
        (3, 2, 2): 0,
        (4, 2, 0): 1,
        (4, 2, 1): 2,
        (5, 2, 0): 1,
        (5, 2, 1): 2,
        (5, 2, 2): 1,
        (5, 2, 3): 1,
        (5, 2, 4): 1,
    }
    RUB = {
        (1, 1): 2,
        (1, 2): 2,
        (1, 3): 2,
        (1, 4): 2,
        (1, 5): 2,
        (1, 6): 2,
        (1, 7): 2,
        (2, 1): 2,
        (2, 2): 2,
        (2, 3): 2,
        (2, 4): 2,
        (2, 5): 2,
        (2, 6): 2,
        (2, 7): 2,
    }
    return (J, P, R, T, p, c, a, RUB)

(J,P,R,T,p,c,a,RUB) = make_2r()
model = rcs(J,P,R,T,p,c,a,RUB)
model.optimize()
x,s = model.__data

print ("Opt.value=",model.ObjVal)
for (j,t) in x:
    if x[j,t].X > 0.5:
        print (x[j,t].VarName,x[j,t].X) 

for j in s:
    if s[j].X > 0.:
        print (s[j].VarName,s[j].X )

Gurobi Optimizer version 9.5.2 build v9.5.2rc0 (mac64[x86])
Thread count: 8 physical cores, 16 logical processors, using up to 16 threads
Optimize a model with 25 rows, 26 columns and 127 nonzeros
Model fingerprint: 0x164fed55
Variable types: 5 continuous, 21 integer (21 binary)
Coefficient statistics:
  Matrix range     [1e+00, 4e+00]
  Objective range  [2e+00, 6e+00]
  Bounds range     [1e+00, 1e+00]
  RHS range        [1e+00, 2e+00]
Found heuristic solution: objective 23.0000000
Presolve removed 25 rows and 26 columns
Presolve time: 0.00s
Presolve: All rows and columns removed

Explored 0 nodes (0 simplex iterations) in 0.01 seconds (0.00 work units)
Thread count was 1 (of 16 available processors)

Solution count 1: 23 

Optimal solution found (tolerance 1.00e-04)
Best objective 2.300000000000e+01, best bound 2.300000000000e+01, gap 0.0000%
Opt.value= 23.0
x(1,1) 1.0
x(2,3) 1.0
x(3,4) 1.0
x(4,5) 1.0
x(5,1) 1.0
s(2) 2.0
s(3) 3.0
s(4) 4.0

import collections
from typing import Optional

from absl import app
from absl import flags

from google.protobuf import text_format
from ortools.sat.python import cp_model
from ortools.scheduling import rcpsp_pb2
from ortools.scheduling.python import rcpsp

_INPUT = flags.DEFINE_string("input", "", "Input file to parse and solve.")
_OUTPUT_PROTO = flags.DEFINE_string(
    "output_proto", "", "Output file to write the cp_model proto to."
)
_PARAMS = flags.DEFINE_string("params", "", "Sat solver parameters.")
_USE_INTERVAL_MAKESPAN = flags.DEFINE_bool(
    "use_interval_makespan",
    True,
    "Whether we encode the makespan using an interval or not.",
)
_HORIZON = flags.DEFINE_integer("horizon", -1, "Force horizon.")
_ADD_REDUNDANT_ENERGETIC_CONSTRAINTS = flags.DEFINE_bool(
    "add_redundant_energetic_constraints",
    False,
    "add redundant energetic constraints on the pairs of tasks extracted from"
    + " precedence graph.",
)
_DELAY_TIME_LIMIT = flags.DEFINE_float(
    "delay_time_limit",
    20.0,
    "Time limit when computing min delay between tasks."
    + " A non-positive time limit disable min delays computation.",
)
_PREEMPTIVE_LB_TIME_LIMIT = flags.DEFINE_float(
    "preemptive_lb_time_limit",
    0.0,
    "Time limit when computing a preemptive schedule lower bound."
    + " A non-positive time limit disable this computation.",
)


def print_problem_statistics(problem: rcpsp_pb2.RcpspProblem):
    """Display various statistics on the problem."""

    # Determine problem type.
    problem_type = (
        "Resource Investment Problem" if problem.is_resource_investment else "RCPSP"
    )

    num_resources = len(problem.resources)
    num_tasks = len(problem.tasks) - 2  # 2 sentinels.
    tasks_with_alternatives = 0
    variable_duration_tasks = 0
    tasks_with_delay = 0

    for task in problem.tasks:
        if len(task.recipes) > 1:
            tasks_with_alternatives += 1
            duration_0 = task.recipes[0].duration
            for recipe in task.recipes:
                if recipe.duration != duration_0:
                    variable_duration_tasks += 1
                    break
        if task.successor_delays:
            tasks_with_delay += 1

    if problem.is_rcpsp_max:
        problem_type += "/Max delay"
    # We print 2 less tasks as these are sentinel tasks that are not counted in
    # the description of the rcpsp models.
    if problem.is_consumer_producer:
        print(f"Solving {problem_type} with:")
        print(f"  - {num_resources} reservoir resources")
        print(f"  - {num_tasks} tasks")
    else:
        print(f"Solving {problem_type} with:")
        print(f"  - {num_resources} renewable resources")
        print(f"  - {num_tasks} tasks")
        if tasks_with_alternatives:
            print(f"    - {tasks_with_alternatives} tasks with alternative resources")
        if variable_duration_tasks:
            print(f"    - {variable_duration_tasks} tasks with variable durations")
        if tasks_with_delay:
            print(f"    - {tasks_with_delay} tasks with successor delays")


def analyse_dependency_graph(
    problem: rcpsp_pb2.RcpspProblem,
) -> tuple[list[tuple[int, int, list[int]]], dict[int, list[int]]]:
    """Analyses the dependency graph to improve the model.

    Args:
      problem: the protobuf of the problem to solve.

    Returns:
      a list of (task1, task2, in_between_tasks) with task2 and indirect successor
      of task1, and in_between_tasks being the list of all tasks after task1 and
      before task2.
    """

    num_nodes = len(problem.tasks)
    print(f"Analysing the dependency graph over {num_nodes} nodes")

    ins = collections.defaultdict(list)
    outs = collections.defaultdict(list)
    after = collections.defaultdict(set)
    before = collections.defaultdict(set)

    # Build the transitive closure of the precedences.
    # This algorithm has the wrong complexity (n^4), but is OK for the psplib
    # as the biggest example has 120 nodes.
    for n in range(num_nodes):
        for s in problem.tasks[n].successors:
            ins[s].append(n)
            outs[n].append(s)

            for a in list(after[s]) + [s]:
                for b in list(before[n]) + [n]:
                    after[b].add(a)
                    before[a].add(b)

    # Search for pair of tasks, containing at least two parallel branch between
    # them in the precedence graph.
    num_candidates = 0
    result: list[tuple[int, int, list[int]]] = []
    for source, start_outs in outs.items():
        if len(start_outs) <= 1:
            # Starting with the unique successor of source will be as good.
            continue
        for sink, end_ins in ins.items():
            if len(end_ins) <= 1:
                # Ending with the unique predecessor of sink will be as good.
                continue
            if sink == source:
                continue
            if sink not in after[source]:
                continue

            num_active_outgoing_branches = 0
            num_active_incoming_branches = 0
            for succ in outs[source]:
                if sink in after[succ]:
                    num_active_outgoing_branches += 1
            for pred in ins[sink]:
                if source in before[pred]:
                    num_active_incoming_branches += 1

            if num_active_outgoing_branches <= 1 or num_active_incoming_branches <= 1:
                continue

            common = after[source].intersection(before[sink])
            if len(common) <= 1:
                continue
            num_candidates += 1
            result.append((source, sink, common))

    # Sort entries lexicographically by (len(common), source, sink)
    def price(entry):
        return num_nodes * num_nodes * len(entry[2]) + num_nodes * entry[0] + entry[1]

    result.sort(key=price)
    print(f"  - created {len(result)} pairs of nodes to examine", flush=True)
    return result, after


def solve_rcpsp(
    problem: rcpsp_pb2.RcpspProblem,
    proto_file: str,
    params: str,
    active_tasks: set[int],
    source: int,
    sink: int,
    intervals_of_tasks: list[tuple[int, int, list[int]]],
    delays: dict[tuple[int, int], tuple[int, int]],
    in_main_solve: bool = False,
    initial_solution: Optional[rcpsp_pb2.RcpspAssignment] = None,
    lower_bound: int = 0,
) -> tuple[int, int, Optional[rcpsp_pb2.RcpspAssignment]]:
    """Parse and solve a given RCPSP problem in proto format.

    The model will only look at the tasks {source} + {sink} + active_tasks, and
    ignore all others.

    Args:
      problem: the description of the model to solve in protobuf format
      proto_file: the name of the file to export the CpModel proto to.
      params: the string representation of the parameters to pass to the sat
        solver.
      active_tasks: the set of active tasks to consider.
      source: the source task in the graph. Its end will be forced to 0.
      sink: the sink task of the graph. Its start is the makespan of the problem.
      intervals_of_tasks: a heuristic lists of (task1, task2, tasks) used to add
        redundant energetic equations to the model.
      delays: a list of (task1, task2, min_delays) used to add extended precedence
        constraints (start(task2) >= end(task1) + min_delay).
      in_main_solve: indicates if this is the main solve procedure.
      initial_solution: A valid assignment used to hint the search.
      lower_bound: A valid lower bound of the makespan objective.

    Returns:
      (lower_bound of the objective, best solution found, assignment)
    """
    # Create the model.
    model = cp_model.CpModel()
    model.name = problem.name

    num_resources = len(problem.resources)

    all_active_tasks = list(active_tasks)
    all_active_tasks.sort()
    all_resources = range(num_resources)

    horizon = problem.deadline if problem.deadline != -1 else problem.horizon
    if _HORIZON.value > 0:
        horizon = _HORIZON.value
    elif delays and in_main_solve and (source, sink) in delays:
        horizon = delays[(source, sink)][1]
    elif horizon == -1:  # Naive computation.
        horizon = sum(max(r.duration for r in t.recipes) for t in problem.tasks)
        if problem.is_rcpsp_max:
            for t in problem.tasks:
                for sd in t.successor_delays:
                    for rd in sd.recipe_delays:
                        for d in rd.min_delays:
                            horizon += abs(d)
    if in_main_solve:
        print(f"Horizon = {horizon}", flush=True)

    # Containers.
    task_starts = {}
    task_ends = {}
    task_durations = {}
    task_intervals = {}
    task_resource_to_energy = {}
    task_to_resource_demands = collections.defaultdict(list)

    task_to_presence_literals = collections.defaultdict(list)
    task_to_recipe_durations = collections.defaultdict(list)
    task_resource_to_fixed_demands = collections.defaultdict(dict)
    task_resource_to_max_energy = collections.defaultdict(int)

    resource_to_sum_of_demand_max = collections.defaultdict(int)

    # Create task variables.
    for t in all_active_tasks:
        task = problem.tasks[t]
        num_recipes = len(task.recipes)
        all_recipes = range(num_recipes)

        start_var = model.new_int_var(0, horizon, f"start_of_task_{t}")
        end_var = model.new_int_var(0, horizon, f"end_of_task_{t}")

        literals = []
        if num_recipes > 1:
            # Create one literal per recipe.
            literals = [model.new_bool_var(f"is_present_{t}_{r}") for r in all_recipes]

            # Exactly one recipe must be performed.
            model.add_exactly_one(literals)

        else:
            literals = [1]

        # Temporary data structure to fill in 0 demands.
        demand_matrix = collections.defaultdict(int)

        # Scan recipes and build the demand matrix and the vector of durations.
        for recipe_index, recipe in enumerate(task.recipes):
            task_to_recipe_durations[t].append(recipe.duration)
            for demand, resource in zip(recipe.demands, recipe.resources):
                demand_matrix[(resource, recipe_index)] = demand

        # Create the duration variable from the accumulated durations.
        duration_var = model.new_int_var_from_domain(
            cp_model.Domain.from_values(task_to_recipe_durations[t]),
            f"duration_of_task_{t}",
        )

        # Link the recipe literals and the duration_var.
        for r in range(num_recipes):
            model.add(duration_var == task_to_recipe_durations[t][r]).only_enforce_if(
                literals[r]
            )

        # Create the interval of the task.
        task_interval = model.new_interval_var(
            start_var, duration_var, end_var, f"task_interval_{t}"
        )

        # Store task variables.
        task_starts[t] = start_var
        task_ends[t] = end_var
        task_durations[t] = duration_var
        task_intervals[t] = task_interval
        task_to_presence_literals[t] = literals

        # Create the demand variable of the task for each resource.
        for res in all_resources:
            demands = [demand_matrix[(res, recipe)] for recipe in all_recipes]
            task_resource_to_fixed_demands[(t, res)] = demands
            demand_var = model.new_int_var_from_domain(
                cp_model.Domain.from_values(demands), f"demand_{t}_{res}"
            )
            task_to_resource_demands[t].append(demand_var)

            # Link the recipe literals and the demand_var.
            for r in all_recipes:
                model.add(demand_var == demand_matrix[(res, r)]).only_enforce_if(
                    literals[r]
                )

            resource_to_sum_of_demand_max[res] += max(demands)

        # Create the energy expression for (task, resource):
        for res in all_resources:
            task_resource_to_energy[(t, res)] = sum(
                literals[r]
                * task_to_recipe_durations[t][r]
                * task_resource_to_fixed_demands[(t, res)][r]
                for r in all_recipes
            )
            task_resource_to_max_energy[(t, res)] = max(
                task_to_recipe_durations[t][r]
                * task_resource_to_fixed_demands[(t, res)][r]
                for r in all_recipes
            )

    # Create makespan variable
    makespan = model.new_int_var(lower_bound, horizon, "makespan")
    makespan_size = model.new_int_var(1, horizon, "interval_makespan_size")
    interval_makespan = model.new_interval_var(
        makespan,
        makespan_size,
        model.new_constant(horizon + 1),
        "interval_makespan",
    )

    # Add precedences.
    if problem.is_rcpsp_max:
        # In RCPSP/Max problem, precedences are given and max delay (possible
        # negative) between the starts of two tasks.
        for task_id in all_active_tasks:
            task = problem.tasks[task_id]
            num_modes = len(task.recipes)

            for successor_index, next_id in enumerate(task.successors):
                delay_matrix = task.successor_delays[successor_index]
                num_next_modes = len(problem.tasks[next_id].recipes)
                for m1 in range(num_modes):
                    s1 = task_starts[task_id]
                    p1 = task_to_presence_literals[task_id][m1]
                    if next_id == sink:
                        delay = delay_matrix.recipe_delays[m1].min_delays[0]
                        model.add(s1 + delay <= makespan).only_enforce_if(p1)
                    else:
                        for m2 in range(num_next_modes):
                            delay = delay_matrix.recipe_delays[m1].min_delays[m2]
                            s2 = task_starts[next_id]
                            p2 = task_to_presence_literals[next_id][m2]
                            model.add(s1 + delay <= s2).only_enforce_if([p1, p2])
    else:
        # Normal dependencies (task ends before the start of successors).
        for t in all_active_tasks:
            for n in problem.tasks[t].successors:
                if n == sink:
                    model.add(task_ends[t] <= makespan)
                elif n in active_tasks:
                    model.add(task_ends[t] <= task_starts[n])

    # Containers for resource investment problems.
    capacities = []  # Capacity variables for all resources.
    max_cost = 0  # Upper bound on the investment cost.

    # Create resources.
    for res in all_resources:
        resource = problem.resources[res]
        c = resource.max_capacity
        if c == -1:
            print(f"No capacity: {resource}")
            c = resource_to_sum_of_demand_max[res]

        # RIP problems have only renewable resources, and no makespan.
        if problem.is_resource_investment or resource.renewable:
            intervals = [task_intervals[t] for t in all_active_tasks]
            demands = [task_to_resource_demands[t][res] for t in all_active_tasks]

            if problem.is_resource_investment:
                capacity = model.new_int_var(0, c, f"capacity_of_{res}")
                model.add_cumulative(intervals, demands, capacity)
                capacities.append(capacity)
                max_cost += c * resource.unit_cost
            else:  # Standard renewable resource.
                if _USE_INTERVAL_MAKESPAN.value:
                    intervals.append(interval_makespan)
                    demands.append(c)

                model.add_cumulative(intervals, demands, c)
        else:  # Non empty non renewable resource. (single mode only)
            if problem.is_consumer_producer:
                reservoir_starts = []
                reservoir_demands = []
                for t in all_active_tasks:
                    if task_resource_to_fixed_demands[(t, res)][0]:
                        reservoir_starts.append(task_starts[t])
                        reservoir_demands.append(
                            task_resource_to_fixed_demands[(t, res)][0]
                        )
                model.add_reservoir_constraint(
                    reservoir_starts,
                    reservoir_demands,
                    resource.min_capacity,
                    resource.max_capacity,
                )
            else:  # No producer-consumer. We just sum the demands.
                model.add(
                    cp_model.LinearExpr.sum(
                        [task_to_resource_demands[t][res] for t in all_active_tasks]
                    )
                    <= c
                )

    # Objective.
    if problem.is_resource_investment:
        objective = model.new_int_var(0, max_cost, "capacity_costs")
        model.add(
            objective
            == sum(
                problem.resources[i].unit_cost * capacities[i]
                for i in range(len(capacities))
            )
        )
    else:
        objective = makespan

    model.minimize(objective)

    # Add min delay constraints.
    if delays is not None:
        for (local_start, local_end), (min_delay, _) in delays.items():
            if local_start == source and local_end in active_tasks:
                model.add(task_starts[local_end] >= min_delay)
            elif local_start in active_tasks and local_end == sink:
                model.add(makespan >= task_ends[local_start] + min_delay)
            elif local_start in active_tasks and local_end in active_tasks:
                model.add(task_starts[local_end] >= task_ends[local_start] + min_delay)

    problem_is_single_mode = True
    for t in all_active_tasks:
        if len(task_to_presence_literals[t]) > 1:
            problem_is_single_mode = False
            break

    # Add sentinels.
    task_starts[source] = 0
    task_ends[source] = 0
    task_to_presence_literals[0].append(True)
    task_starts[sink] = makespan
    task_to_presence_literals[sink].append(True)

    # For multi-mode problems, add a redundant energetic constraint:
    # for every (start, end, in_between_tasks) extracted from the precedence
    # graph, it add the energetic relaxation:
    #   (start_var('end') - end_var('start')) * capacity_max >=
    #        sum of linearized energies of all tasks from 'in_between_tasks'
    if (
        not problem.is_resource_investment
        and not problem.is_consumer_producer
        and _ADD_REDUNDANT_ENERGETIC_CONSTRAINTS.value
        and in_main_solve
        and not problem_is_single_mode
    ):
        added_constraints = 0
        ignored_constraits = 0
        for local_start, local_end, common in intervals_of_tasks:
            for res in all_resources:
                resource = problem.resources[res]
                if not resource.renewable:
                    continue
                c = resource.max_capacity
                if delays and (local_start, local_end) in delays:
                    min_delay, _ = delays[local_start, local_end]
                    sum_of_max_energies = sum(
                        task_resource_to_max_energy[(t, res)] for t in common
                    )
                    if sum_of_max_energies <= c * min_delay:
                        ignored_constraits += 1
                        continue
                model.add(
                    c * (task_starts[local_end] - task_ends[local_start])
                    >= sum(task_resource_to_energy[(t, res)] for t in common)
                )
                added_constraints += 1
        print(
            f"Added {added_constraints} redundant energetic constraints, and "
            + f"ignored {ignored_constraits} constraints.",
            flush=True,
        )

    # Add solution hint.
    if initial_solution:
        for t in all_active_tasks:
            model.add_hint(task_starts[t], initial_solution.start_of_task[t])
            if len(task_to_presence_literals[t]) > 1:
                selected = initial_solution.selected_recipe_of_task[t]
                model.add_hint(task_to_presence_literals[t][selected], 1)

    # Write model to file.
    if proto_file:
        print(f"Writing proto to{proto_file}")
        model.export_to_file(proto_file)

    # Solve model.
    solver = cp_model.CpSolver()

    # Parse user specified parameters.
    if params:
        text_format.Parse(params, solver.parameters)

    # Favor objective_shaving_search over objective_lb_search.
    if solver.parameters.num_workers >= 16 and solver.parameters.num_workers < 24:
        solver.parameters.ignore_subsolvers.append("objective_lb_search")
        solver.parameters.extra_subsolvers.append("objective_shaving_search")

    # Experimental: Specify the fact that the objective is a makespan
    solver.parameters.push_all_tasks_toward_start = True

    # Enable logging in the main solve.

    if in_main_solve:
        solver.parameters.log_search_progress = True
    #
    status = solver.solve(model)
    if status == cp_model.OPTIMAL or status == cp_model.FEASIBLE:
        assignment = rcpsp_pb2.RcpspAssignment()
        for t, _ in enumerate(problem.tasks):
            if t in task_starts:
                assignment.start_of_task.append(solver.value(task_starts[t]))
                for r, recipe_literal in enumerate(task_to_presence_literals[t]):
                    if solver.boolean_value(recipe_literal):
                        assignment.selected_recipe_of_task.append(r)
                        break
            else:  # t is not an active task.
                assignment.start_of_task.append(0)
                assignment.selected_recipe_of_task.append(0)
        return (
            int(solver.best_objective_bound),
            int(solver.objective_value),
            assignment,
        )
    return -1, -1, None


def compute_delays_between_nodes(
    problem: rcpsp_pb2.RcpspProblem,
    task_intervals: list[tuple[int, int, list[int]]],
) -> tuple[
    dict[tuple[int, int], tuple[int, int]],
    Optional[rcpsp_pb2.RcpspAssignment],
    bool,
]:
    """Computes the min delays between all pairs of tasks in 'task_intervals'.

    Args:
      problem: The protobuf of the model.
      task_intervals: The output of the AnalysePrecedenceGraph().

    Returns:
      a list of (task1, task2, min_delay_between_task1_and_task2)
    """
    print("Computing the minimum delay between pairs of intervals")
    delays = {}
    if (
        problem.is_resource_investment
        or problem.is_consumer_producer
        or problem.is_rcpsp_max
        or _DELAY_TIME_LIMIT.value <= 0.0
    ):
        return delays, None, False

    complete_problem_assignment = None
    num_optimal_delays = 0
    num_delays_not_found = 0
    optimal_found = True
    for start_task, end_task, active_tasks in task_intervals:
        min_delay, feasible_delay, assignment = solve_rcpsp(
            problem,
            "",
            f"num_search_workers:16,max_time_in_seconds:{_DELAY_TIME_LIMIT.value}",
            set(active_tasks),
            start_task,
            end_task,
            [],
            delays,
        )
        if min_delay != -1:
            delays[(start_task, end_task)] = min_delay, feasible_delay
            if start_task == 0 and end_task == len(problem.tasks) - 1:
                complete_problem_assignment = assignment
            if min_delay == feasible_delay:
                num_optimal_delays += 1
            else:
                optimal_found = False
        else:
            num_delays_not_found += 1
            optimal_found = False

    print(f"  - #optimal delays = {num_optimal_delays}", flush=True)
    if num_delays_not_found:
        print(f"  - #not computed delays = {num_delays_not_found}", flush=True)

    return delays, complete_problem_assignment, optimal_found


def accept_new_candidate(
    problem: rcpsp_pb2.RcpspProblem,
    after: dict[int, list[int]],
    demand_map: dict[tuple[int, int], int],
    current: list[int],
    candidate: int,
) -> bool:
    """Check if candidate is compatible with the tasks in current."""
    for c in current:
        if candidate in after[c] or c in after[candidate]:
            return False

    all_resources = range(len(problem.resources))
    for res in all_resources:
        resource = problem.resources[res]
        if not resource.renewable:
            continue
        if (
            sum(demand_map[(t, res)] for t in current) + demand_map[(candidate, res)]
            > resource.max_capacity
        ):
            return False

    return True


def compute_preemptive_lower_bound(
    problem: rcpsp_pb2.RcpspProblem,
    after: dict[int, list[int]],
    lower_bound: int,
) -> int:
    """Computes a preemtive lower bound for the makespan statically.

    For this, it breaks all intervals into a set of intervals of size one.
    Then it will try to assign all of them in a minimum number of configurations.
    This is a standard complete set covering using column generation approach
    where each column is a possible combination of itervals of size one.

    Args:
      problem: The probuf of the model.
      after: a task to list of task dict that contains all tasks after a given
        task.
      lower_bound: A valid lower bound of the problem. It can be 0.

    Returns:
      a valid lower bound of the problem.
    """
    # Check this is a single mode problem.
    if (
        problem.is_rcpsp_max
        or problem.is_resource_investment
        or problem.is_consumer_producer
    ):
        return lower_bound

    demand_map = collections.defaultdict(int)
    duration_map = {}
    all_active_tasks = list(range(1, len(problem.tasks) - 1))
    max_duration = 0
    sum_of_demands = 0

    for t in all_active_tasks:
        task = problem.tasks[t]
        if len(task.recipes) > 1:
            return 0
        recipe = task.recipes[0]
        duration_map[t] = recipe.duration
        for demand, resource in zip(recipe.demands, recipe.resources):
            demand_map[(t, resource)] = demand
            max_duration = max(max_duration, recipe.duration)
            sum_of_demands += demand

    print(
        f"Compute a bin-packing lower bound with {len(all_active_tasks)}"
        + " active tasks",
        flush=True,
    )
    all_combinations = []

    for t in all_active_tasks:
        new_combinations = [[t]]

        for c in all_combinations:
            if accept_new_candidate(problem, after, demand_map, c, t):
                new_combinations.append(c + [t])

        all_combinations.extend(new_combinations)

    print(f"  - created {len(all_combinations)} combinations")
    if len(all_combinations) > 5000000:
        return lower_bound  # Abort if too large.

    # solve the selection model.

    # TODO(user): a few possible improvements:
    # 1/  use "dominating" columns, i.e. if you can add a task to a column, then
    #     do not use that column.
    # 2/ Merge all task with exactly same demands into one.
    model = cp_model.CpModel()
    model.name = f"lower_bound_{problem.name}"

    vars_per_task = collections.defaultdict(list)
    all_vars = []
    for c in all_combinations:
        min_duration = max_duration
        for t in c:
            min_duration = min(min_duration, duration_map[t])
        count = model.new_int_var(0, min_duration, f"count_{c}")
        all_vars.append(count)
        for t in c:
            vars_per_task[t].append(count)

    # Each task must be performed.
    for t in all_active_tasks:
        model.add(sum(vars_per_task[t]) >= duration_map[t])

    # Objective
    objective_var = model.new_int_var(lower_bound, sum_of_demands, "objective_var")
    model.add(objective_var == sum(all_vars))

    model.minimize(objective_var)

    # solve model.
    solver = cp_model.CpSolver()
    solver.parameters.num_search_workers = 16
    solver.parameters.max_time_in_seconds = _PREEMPTIVE_LB_TIME_LIMIT.value
    status = solver.solve(model)
    if status == cp_model.OPTIMAL or status == cp_model.FEASIBLE:
        status_str = "optimal" if status == cp_model.OPTIMAL else ""
        lower_bound = max(lower_bound, int(solver.best_objective_bound))
        print(f"  - {status_str} static lower bound = {lower_bound}", flush=True)

    return lower_bound


def main(_):
    rcpsp_parser = rcpsp.RcpspParser()
    rcpsp_parser.parse_file(_INPUT.value)

    problem = rcpsp_parser.problem()
    print_problem_statistics(problem)

    intervals_of_tasks, after = analyse_dependency_graph(problem)
    delays, initial_solution, optimal_found = compute_delays_between_nodes(
        problem, intervals_of_tasks
    )

    last_task = len(problem.tasks) - 1
    key = (0, last_task)
    lower_bound = delays[key][0] if key in delays else 0
    if not optimal_found and _PREEMPTIVE_LB_TIME_LIMIT.value > 0.0:
        lower_bound = compute_preemptive_lower_bound(problem, after, lower_bound)

    solve_rcpsp(
        problem=problem,
        proto_file=_OUTPUT_PROTO.value,
        params=_PARAMS.value,
        active_tasks=set(range(1, last_task)),
        source=0,
        sink=last_task,
        intervals_of_tasks=intervals_of_tasks,
        delays=delays,
        in_main_solve=True,
        initial_solution=initial_solution,
        lower_bound=lower_bound,
    )

rcpsp_parser = rcpsp.RcpspParser()