COPTによる非線形最適化問題のモデリング

COPTを用いた非線形最適化のモデリングのコツについて述べる．

from amplpy import AMPL, Environment
env = Environment("/Users/mikiokubo/Documents/ampl/")
ampl = AMPL(env)

COPT

COPT (Cardinal Optimizer) は、近年急速にシェアを伸ばしている高性能な商用ソルバーで、LP/MIPだけでなく、SOCP（二次錐計画） や SDP（半正定値計画） の性能も非常に高いのが特徴です。

AMPLからCOPTを使用してロバストポートフォリオ問題を解く方法を解説します。

1. ソルバーの指定

AMPLでCOPTを呼び出すには、option solver を設定するだけです。AMPL MPライブラリ経由で、最新の錐計画構文（in PSD, in SOC）をそのまま利用できます。

option solver copt;

2. ロバストポートフォリオの定式化 (SOCP形式)

ロバストポートフォリオ（特に期待収益率の不確実性を考慮する場合）は、SDPよりも計算負荷の低い SOCP（二次錐計画） として記述するのが一般的です。COPTはこのSOCPの計算において非常に強力なベンチマーク結果を出しています。

def solve_with_copt():
    ampl = AMPL(env)
    
    # 1. ソルバーをCOPTに設定
    ampl.set_option('solver', 'copt')
    ampl.set_option('copt_options', 'outlev=0')
    ampl.set_option('solver_msg', 0)
    # COPT固有のオプション（例：スレッド数やアルゴリズムの指定）
    # ampl.set_option('copt_options', 'threads=4 method=2') 

    ampl.eval('''
        set ASSETS;
        param mu {ASSETS};
        param R_target;
        param delta;
        var w {ASSETS} >= 0;
        var risk_var >= 0;

        minimize Portfolio_Risk: risk_var;

        subject to Budget:
            sum {i in ASSETS} w[i] = 1;

        subject to Robust_Constraint:
            sum {i in ASSETS} mu[i] * w[i] - delta * risk_var >= R_target;
            
        # SOCP制約
        subject to Cone: sum {i in ASSETS} w[i]^2 <= risk_var^2;
    ''')

    # データのセットアップ
    assets = ['AAPL', 'GOOGL', 'MSFT']
    ampl.get_set('ASSETS').set_values(assets)
    ampl.get_parameter('mu').set_values({'AAPL': 0.12, 'GOOGL': 0.15, 'MSFT': 0.10})
    ampl.get_parameter('R_target').set(0.1)
    ampl.get_parameter('delta').set(0.05)

    # 実行
    ampl.solve()

    # 結果取得
    weights = ampl.get_variable('w').get_values().to_pandas()
    print("Optimization Results with COPT:")
    print(weights)

if __name__ == "__main__":
    solve_with_copt()

COPT 7.2.4:   tech:outlev = 0
Optimization Results with COPT:
          w.val
AAPL   0.314183
GOOGL  0.487061
MSFT   0.198756

感度分析

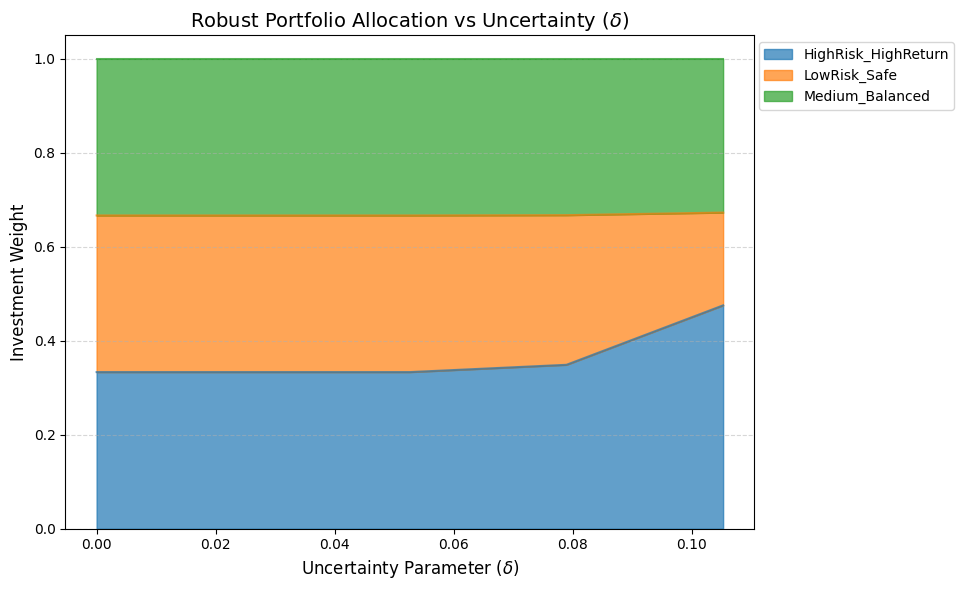
不確実性パラメータ \(\delta\) を変化させたときに、ポートフォリオの資産配分がどのように変化するかを可視化する感度分析スクリプトを作成します。

この分析を行うことで、「予測が外れるリスクをどれだけ許容するか（ロバスト性の強さ）」によって、投資戦略がどう保守的になっていくかを直感的に理解できます。

ロバスト性の感度分析：Pythonスクリプトこのコードでは、\(\delta\)（不確実性の円の半径）を 0.0（標準的なモデル）から段階的に増やし、各ポイントでの配分比率を計算します。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

def run_robust_sensitivity():
    ampl = AMPL(env)
    ampl.set_option('solver', 'copt')
    ampl.set_option('copt_options', 'outlev=0')
    ampl.set_option('solver_msg', 0)

    # 1. AMPLモデルの定義
    # ここでは期待収益率の不確実性（楕円集合）を考慮したSOCPモデルを使用
    ampl.eval('''
        set ASSETS;
        param mu {ASSETS};
        param R_target;
        param delta; # 不確実性パラメータ
        
        var w {ASSETS} >= 0;
        var risk_var >= 0;

        minimize Portfolio_Risk: risk_var;

        subject to Budget:
            sum {i in ASSETS} w[i] = 1;

        subject to Robust_Constraint:
            sum {i in ASSETS} mu[i] * w[i] - delta * risk_var >= R_target;
            
        subject to Cone: sum {i in ASSETS} w[i]^2 <= risk_var^2;
    ''')

    # 2. サンプルデータの用意
    assets = ['HighRisk_HighReturn', 'Medium_Balanced', 'LowRisk_Safe']
    ampl.get_set('ASSETS').set_values(assets)
    ampl.get_parameter('mu').set_values({
        'HighRisk_HighReturn': 0.20, 
        'Medium_Balanced': 0.12, 
        'LowRisk_Safe': 0.05
    })
    ampl.get_parameter('R_target').set(0.08)

    # 3. デルタ（不確実性）をスイープさせる
    delta_values = np.linspace(0, 0.5, 20)
    results = []

    for d in delta_values:
        ampl.get_parameter('delta').set(d)
        ampl.solve()
        
        # 最適解が得られた場合のみデータを保存
        if ampl.get_value('solve_result') == 'solved':
            w_values = ampl.get_variable('w').get_values().to_dict()
            w_values['delta'] = d
            results.append(w_values)

    # 4. 可視化
    df_results = pd.DataFrame(results).set_index('delta')
    
    plt.figure(figsize=(10, 6))
    df_results.plot.area(stacked=True, alpha=0.7, ax=plt.gca())
    plt.title(r'Robust Portfolio Allocation vs Uncertainty ($\delta$)', fontsize=14)
    plt.xlabel(r'Uncertainty Parameter ($\delta$)', fontsize=12)
    plt.ylabel('Investment Weight', fontsize=12)
    plt.legend(loc='upper right', bbox_to_anchor=(1.3, 1))
    plt.grid(axis='y', linestyle='--', alpha=0.5)
    plt.tight_layout()
    plt.show()

if __name__ == "__main__":
    run_robust_sensitivity()

COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0
COPT 7.2.4:   tech:outlev = 0